Машинное обучение : базовые алгоритмы.

Тема очень обширная, и в один пост все, что стоило бы сказать, не влезет. Так что в этом посте постараемся разобраться, что же такое машоб, и как он вообще делается. Если читателям понравится – напишу по этой теме еще.

Итак, чтобы понять, как учатся машины, давайте для начала вспомним, как учимся мы - на примере первоклашки, которому рассказывают про алфавит.
Как все выглядит? Сначала ему показывают непонятную для него закорючку и говорят: "Вот это буква а. ААА. Запомнил?" Потом идет новая закорючка: "Бээээ". И так до конца.
Скоро все буквы пиздюку показаны, и учитель, довольный собой, показывает букву "а" опять. "Что за буква?"
Почти наверняка ребенок не ответит. Почему? Так мало примеров! Надо бы повторить. И так, раз за разом, мы показываем ему буквы, пока он все не усвоит. Так он запоминает значение каждой закорючки.
А дальше мы начинаем показывать ему рукописные буквы, всех форм и размеров, и малыш опять теряется, ведь он привык к ровным, красивым и печатным. Еще немало времени пройдет, прежде чем он сможет уверенно понимать различные написания. Так происходит обобщение.

Итак, что тут произошло? А вот что. Сперва ребенок видел перед собой просто странные символы, понятия о которых у него не было. После 3-4 проходов по алфавиту он начал замечать отличительные черты букв – у "а" кружочек с хвостиком, у "ж" восемь лапок, "к" – похожа на башмак. Дальше эти знания закреплялись, а в конце – обобщались.

Хорошо, перейдем теперь к машине. Как научить ее различать буквы? С печатными все более-менее просто – загружаем в память изображения букв, а поступающие новые просто попиксельно сравниваем с эталоном. Но что делать с прописными? Все варианты мы никогда в жизни не сможем собрать.
Окей, становится сложно. Нужна идея, желательно извне, потому что думать самому – сложно и скучно.
Подсмотрим у природы. Как обучался ребенок? Он выделял паттерны в изображениях. Кружочки и закорючки. Так давайте придумаем способ научить машину выделять такие паттерны!

И вот мы пришли к тому, что такое машинное обучение – это написание алгоритмов, способных находить, обобщать и экстраполировать (выводить) закономерности в данных.

Отлично, определение – это уже половина дела. Теперь надо придумать, как же научить машину извлекать эти паттерны, а еще перед этим – как же данные машине подать.
Тут к нам на помощь приходит математика – искусство называть разные вещи одним и тем же именем, как говорил великий Пуанкаре.

Каким образом можно описать какой-то объект? Давайте посмотрим, какие у него есть отличительные черты. Возьмем, например, цветок ириса и измерим в нескольких (например, 4) местах его лепестки. Запишем эти цифры и забудем, что же мы измеряли. Тогда цветок станет просто набором из 4 цифр (x1, x2, x3, x4). По сути – вектором, который называют признаковым описанием объекта. Такой вид идеально подходит для машины – все лаконично, и никакой лишней информации. Но для себя отметим, что же мы отмеряли, чтобы в будущем не перепутать, и сохраним в качестве второй картинки к посту.
Продолжим измерять цветки, каждый раз записывая новый вектор под старыми. Так мы получим двумерную таблицу из чисел – матрицу объектов-признаков, и обозначим ее Х.
А теперь отнесем все измеренные соцветия флористам, чтобы они сказали нам, какого сорта каждый цветок. Занумеруем их и получим вектор, в котором столько же элементов, сколько строк в матрице – вектор ответов Y.
Теперь совместим Х с Y, и на третьей пикче увидим, что же нас вышло.

Конечно, придумал это не я (потому что придумывать что-то сложно и скучно), а математик Фишер, чтобы продемонстрировать мощь своего математического колдунства (это было почти машинное обучение, только ручками на бумаге). С тех пор этот пример стал классическим, а про Ирисы Фишера есть даже статья в вики, которую интересующиеся могут просмотреть. Ну или хотя бы глянуть на третью картинку, чтобы яснее представлять себе, что у нас получилось

Итак, что мы имеем? Есть признаковое описание множества объектов Х. Есть вектор ответов Y. Теперь осталось придумать, как же научить машину определять, какой ответ давать для конкретного объекта, опираясь на имеющиеся данные. Звучит просто (нет).

Но пост что-то и так слишком разросся, так что оставим это для лучших времен. Пишите, понравился ли вам пост, стоит ли продолжать, и что стоило бы исправить – буду рад конструктивной критике.

В прошлом посте мы сформулировали, что такое машинное обучение и придумали способ подавать машине данные об окружающем мире. В этом попробуем придумать несложные алгоритмы, позволяющие извлекать закономерности из данных. Алгоритмы получатся довольно простые, но необходимые, чтобы перейти к чему-то более интересному – нейросетям (которые для пидоров) и композициям алгоритмов. В посте будет чутка математики, так что готовьтесь пролистывать ее к хуям – все равно нихера не ясно. Но в ней заключена парочка идей, которые используются не только в машобе, но и в экономике, физике, да и вообще в значительной части вычислений, и кому-то может быть интересно. Да и вообще, в математике весь сок машинного обучения.

Итак, в самом начале нашего пути мы собрали наш первый массив данных – или, как говорят крутые пацаны, датасет – измерения соцветий ириса разных сортов. Записали их в виде матрицы и отложили до лучших времен. Теперь же для простоты представим, что половину наших данных съела собака, и у нас осталась только информация о длине и ширине соцветия, а так же к какому сорту каждый цветок относится. От безысходности отметим на миллиметровке точки, по оси х отложив длину, а по оси у – ширину цветка. Сорт будем отмечать цветом. Результат – наверху первой картинки.

В принципе, есть хорошая новость – явно видно, что один из сортов отлично отделяется от двух других, и можно на глаз провести прямую, разделяющую облака точек. Да вот только компьютер "на глаз" ничего сделать не может. Как же быть?

Чтобы ответить на этот вопрос, решим сначала другую задачу - по длине попробовать предсказать ширину лепестка – это типичная задача регрессии – восстановления непрерывной величины по некоторым данным. Опять прикинем на глаз, как это сделать. В принципе, видим, что точки вытянуты вдоль некоторой прямой. Чтож, проведем некоторую прямую с формулой y = a*x + k, и подставляя х будем получать оценку у. Теперь вопрос - как найти оптимальную прямую?

Введем новое понятие: функция потерь – это функция от данных и предсказаний нашего алгоритма, которая тем меньше, чем лучше качество нашего алгоритма.

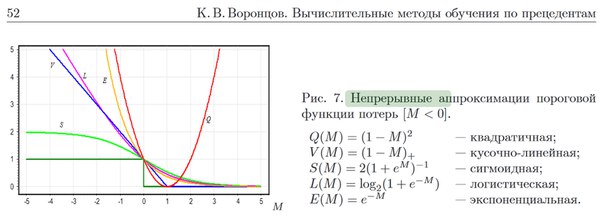
Таких функций придумано дохуя и маленькая тележка, но для регрессии самая классика - это квадратичная функция потерь: sum((y_ - y)^2). На второй картинке ее можно посмотреть глазами – это сумма квадратов отклонений значений величины от нашей кривой. Там же нарисована парабола – зависимость ошибки от величины k.

Очевидно, мы хотим ошибку минимизировать. Мы все тут взрослые ребята, и знаем, что минимум функции находится там, где производная функции равна нулю. Тогда можно в лоб решить несложное уравнение, и узнать оптимальный k. Но у нас тут простой случай, который в жизни почти никогда не встречается – всего одна переменная, хотя обычно их от нескольких десятков до десятков или даже сотен тысяч. Тогда у нас уже будет не красивая формула y = a*x + k, а жуткая sum_i(w_i*x_i ) + w0 = + w0 (скобочки означают скалярное умножение векторов w и x). Что делать тогда?

Тут надо вспомнить, что такое градиент. Вам про него уже писали где-то внизу. Так вот, есть у градиента замечательное свойство – он указывает в сторону наискорейшего убывания функции. То есть, прибавляя к вектору w вектор градиента, мы будем спускаться вниз функции потерь, и в конце достигнем минимума! Собственно, на гифках процесс градиентного спуска можно посмотреть вживую.

Но тут у наc задача классификации, а не регрессии, и квадратичная функция потерь подходит не очень. Поэтому придумали кучу других функций, посмотреть их можно на третьей картинке. У каждой свои плюсы и минусы, но если вдаваться в подробности, то и так слишком большой пост можно будет превратить в серию книг.

Сверху я рассказал про линейные методы – те, которые нередко применяют в продакшене в силу их простоты и возможности работать с лютыми объемами данных (например, в задачах анализа текстов у нас могут быть десятки тысяч признаков и миллионы объектов, и выкатить в прод что-то сложнее линейных моделей зачастую очень затруднительно). Теперь вкратце посмотрим на решающие деревья – логический алгоритм классификации, который сам по себе очень плох, но вот объединение деревьев в "леса" дает очень хорошие результаты.

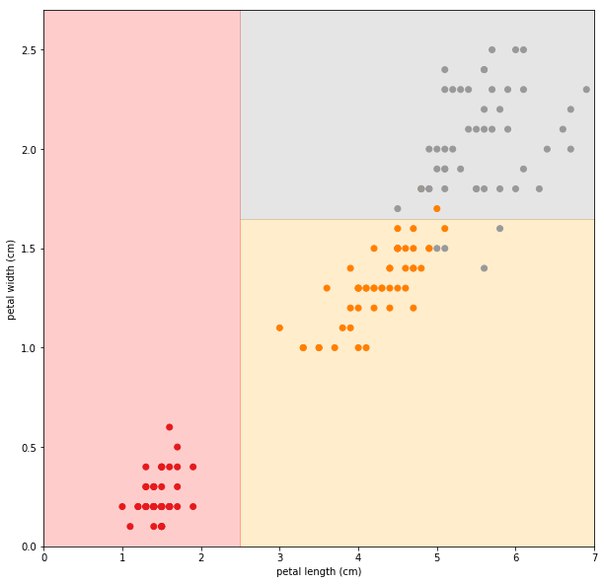
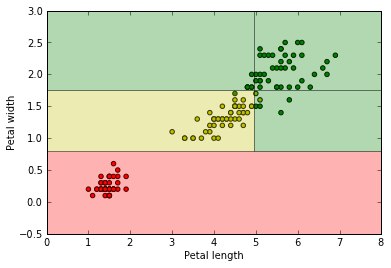
Собственно, глядя на картинку можно заметить такую закономерность – если длина меньше 2.5 см, то точки красные, если больше, но ширина меньше 1.5, то точки, скорее всего, рыжие, иначе – серые. Таки все, дерево готово, и его ленивое изображение можно видеть на четвертом рисунке. А на пятом – как это дерево делит наши точки. Ну и напоследок – какое дерево строит компьютер.

Как он его строит? Сейчас будет самый охуенный и скучный ответ: ПЕРЕБОРОМ. На каждом уровне он перебирает все возможные разделени точек, и смотрит, какое из них сильнее всего уменьшит ошибку, после чего начинает таким же образом строить следующие уровни.

Ух бля, опять лонгрид вышел. Постараюсь в следующий раз такого не допустить. А в следующий раз у нас, между тем, нейросети (которые для пидоров). И там уже более ясно будет видно, как же компьютер находит все эти кружочки и закорючки, про которые говорилось в первой части.

Спасибо за то, что вы с нами.

С любовью, Рителлинг??

Источник: vk.com

Комментарии: