Линейная регрессия с помощью Go

Долгое время меня интересовала тема машинного обучения. Меня удивляло, как машины могут обучаться и прогнозировать безо всякого программирования — поразительно! Я всегда был очарован этим, однако никогда не изучал тему подробно. Время — ресурс скудный, и каждый раз, когда я пытался почитать о машинном обучении, меня заваливало информацией. Освоение всего этого казалось трудным и требовало много времени. Также я убедил себя, что у меня нет необходимых математических знаний даже для того, чтобы начать вникать в машинное обучение.

Но в конце концов я решил подойти к этому иначе. Мало-помалу я буду пытаться воссоздавать в коде разные концепции, начиная с основ и постепенно переходя к более сложным, стараясь охватить как можно больше базовых вещей. В качестве языка я выбрал Go, это один из моих любимых языков, к тому же я не знаком с традиционными для машинного обучения языками вроде R или Python.

Начинаем

Начнём с создания простой модели, чтобы понять, из каких этапов стоит основной процесс обучения.

Допустим, нужно спрогнозировать цены на дома в округе Кинг, штат Вашингтон.

Сначала нужно найти датасет с реальной статистикой. На его основе мы будем создавать модель.

Воспользуемся датасетом с kaggle.

Он идёт в виде csv-файла с такой структурой:

kc_house_data.csv

id,date,price,bedrooms,bathrooms,sqft_living,sqft_lot,floors,waterfront,view,condition,grade,sqft_above,sqft_basement,yr_built,yr_renovated,zipcode,lat,long,sqft_living15,sqft_lot15 "7129300520","20141013T000000",221900,3,1,1180,5650,"1",0,0,3,7,1180,0,1955,0,"98178",47.5112,-122.257,1340,5650 "6414100192","20141209T000000",538000,3,2.25,2570,7242,"2",0,0,3,7,2170,400,1951,1991,"98125",47.721,-122.319,1690,7639 "5631500400","20150225T000000",180000,2,1,770,10000,"1",0,0,3,6,770,0,1933,0,"98028",47.7379,-122.233,2720,8062

Внутри файла есть всё необходимое. Каждый ряд содержит много информации, и придётся разобраться, что именно поможет нам прогнозировать цены на дома.
Нам нужно:

1. Выбрать модель.
2. Разобраться в данных.
3. Подготовить данные к работе.
4. Обучить модель.
5. Протестировать модель.
6. Визуализировать модель.

1. Выбор модели

Воспользуемся одной из простейших популярных моделей — линейно-регрессионной.

Эта модель лежит в основе многих других, и с неё хорошо начинать новый анализ данных. Если получившаяся модель будет прогнозировать достаточно хорошо, то не придётся переходить к более сложной.

Давайте подробнее рассмотрим линейную регрессию:

Этот график показывает взаимосвязь между двумя переменными.

Вертикальная ось (Y) отражает зависимую переменную — в нашем случае цены на дома. Горизонтальная ось (X) отражает так называемую независимую переменную — в нашем случае это могут быть любые другие данные из датасета, например bedrooms, bathrooms, sqft_living...

Круги на графике — y-значения для данного x-значения (y зависит от x). Красная линия — линейная регрессия. Эта линия проходит через все значения и может использовать для прогнозирования возможных значений y для данного x.

Наша цель — обучить модель строить красную линию для нашей задачи.

Напомним, что линейная функция имеет вид y = ax + b. Её нам и нужно найти. Точнее, нам нужно найти такие значения a и b, которые лучше всего удовлетворяют нашим данным.

2. Разбираемся с данными

Мы знаем, какая нам нужна модель и какой подход будем использовать. Осталось проанализировать данные и понять, подходят ли они под нашу задачу.

Данные для линейно-регрессионной модели должны быть нормально распределены. То есть гистограмма данных должна иметь форму колокола.

Давайте построим график на основе наших данных и посмотрим, распределены ли они нужным образом. Для этого наконец-то напишем код!

Полезные пакеты:

• encoding/csv из стандартной библиотеки поможет нам загрузить датасет и разобрать его содержимое.
• github.com/gonum/plot поможет построить график.

Этот код открывает наш CSV и рисует гистограммы для всех колонок, за исключением ID и Date. Tак мы можем выбрать, какие колонки использовать для обучения модели:

    // we open the csv file from the disk         f, err := os.Open("./datasets/kc_house_data.csv")         if err != nil {                 log.Fatal(err)         }         defer f.Close()          // we create a new csv reader specifying         // the number of columns it has         salesData := csv.NewReader(f)         salesData.FieldsPerRecord = 21          // we read all the records         records, err := salesData.ReadAll()         if err != nil {                 log.Fatal(err)         }         // by slicing the records we skip the header         records = records[1:]          // we iterate over all the records         // and keep track of all the gathered values         // for each column         columnsValues := map[int]plotter.Values{}         for i, record := range records {                 // we want one histogram per column,                 // so we will iterate over all the columns we have                 // and gather the date for each in a separate value set                 // in columnsValues                 // we are skipping the ID column and the Date,                 // so we start on index 2                 for c := 2; c < salesData.FieldsPerRecord; c++ {                         if _, found := columnsValues[c]; !found {                                 columnsValues[c] = make(plotter.Values, len(records))                         }                         // we parse each close value and add it to our set                         floatVal, err := strconv.ParseFloat(record[c], 64)                         if err != nil {                                 log.Fatal(err)                         }                         columnsValues[c][i] = floatVal                 }         }          // once we have all the data, we draw each graph         for c, values := range columnsValues {                 // create a new plot                 p, err := plot.New()                 if err != nil {                         log.Fatal(err)                 }                 p.Title.Text = fmt.Sprintf("Histogram of %s", records[0][c])                  // create a new normalized histogram                 // and add it to the plot                 h, err := plotter.NewHist(values, 16)                 if err != nil {                         log.Fatal(err)                 }                 h.Normalize(1)                 p.Add(h)                  // save the plot to a PNG file.                 if err := p.Save(                         10*vg.Centimeter,                         10*vg.Centimeter,                         fmt.Sprintf("./graphs/%s_hist.png", records[0][c]),                 ); err != nil {                         log.Fatal(err)                 }         }

Этот код генерирует набор графиков. Из них нужно выбрать один, больше всего удовлетворяющий условиям нормального распределения (кривая в форме колокола).

Вот какой график выбрал я (все гистограммы):

Это график для колонки Grade. Он не идеален с точки зрения нормального распределения, но пока что этого достаточно. Если посмотрите все гистограммы, то найдёте ещё несколько, которые тоже можно использовать. Если получившаяся модель будет плохо прогнозировать, то выберем за основу другую колонку датасета.

Если что: Grad — это оценка уровня качества здания. Подробнее об уровнях качества зданий можно почитать здесь, в разделе BUILDING GRADE.

3. Подготавливаем данные

Итак, для обучения модели мы будем использовать скачанный датасет. Но как узнать, достаточно ли точная наша модель?

Давайте её протестируем, и для этого воспользуемся тем же датасетом. Чтобы один датасет пригодился для обучения и тестирования, разделим его на две части: одну для обучения, вторую для тестирования. Это нормальный подход.

Обучать будем на 80 % данных, а остальные 20 % возьмём для теста. Есть и другие устоявшиеся соотношения, но для выбора подходящего варианта, скорее всего, придётся действовать методом проб и ошибок.

Нам нужно найти баланс между достаточностью данных для корректного обучения и тестирования, чтобы не переобучить модель.

    // we open the csv file from the disk     f, err := os.Open("./datasets/kc_house_data.csv")     if err != nil {         log.Fatal(err)     }     defer f.Close()      // we create a new csv reader specifying     // the number of columns it has     salesData := csv.NewReader(f)     salesData.FieldsPerRecord = 21      // we read all the records     records, err := salesData.ReadAll()     if err != nil {         log.Fatal(err)     }      // save the header     header := records[0]      // we have to shuffle the dataset before splitting     // to avoid having ordered data     // if the data is ordered, the data in the train set     // and the one in the test set, can have different     // behavior     shuffled := make([][]string, len(records)-1)     perm := rand.Perm(len(records) - 1)     for i, v := range perm {         shuffled[v] = records[i+1]     }      // split the training set     trainingIdx := (len(shuffled)) * 4 / 5     trainingSet := shuffled[1 : trainingIdx+1]      // split the testing set     testingSet := shuffled[trainingIdx+1:]      // we write the splitted sets in separate files     sets := map[string][][]string{         "./datasets/training.csv": trainingSet,         "./datasets/testing.csv":  testingSet,     }      for fn, dataset := range sets {         f, err := os.Create(fn)         if err != nil {             log.Fatal(err)         }         defer f.Close()          out := csv.NewWriter(f)         if err := out.Write(header); err != nil {             log.Fatal(err)         }          if err := out.WriteAll(dataset); err != nil {             log.Fatal(err)         }         out.Flush()     }

Приведённый код генерирует два файла:

• training.csv — содержит записи для обучения модели.
• testing.csv — содержит записи для тестирования.

4. Обучаем модель

Теперь приступим к обучению. Для этого годятся разные пакеты, мы возьмём github.com/sajari/regression, в нём реализовано всё необходимое.

Конечно, можно написать всё с нуля, но пока не будем усложнять.

Сначала скачаем записи из training.csv, пройдём по ним и положим в модель данные из колонок Price и Grade.

Теперь обучим модель находить нашу линейную функцию.

Этим займётся код:

    // we open the csv file from the disk     f, err := os.Open("./datasets/training.csv")     if err != nil {         log.Fatal(err)     }     defer f.Close()      // we create a new csv reader specifying     // the number of columns it has     salesData := csv.NewReader(f)     salesData.FieldsPerRecord = 21      // we read all the records     records, err := salesData.ReadAll()     if err != nil {         log.Fatal(err)     }      // In this case we are going to try and model our house price (y)     // by the grade feature.     var r regression.Regression     r.SetObserved("Price")     r.SetVar(0, "Grade")      // Loop of records in the CSV, adding the training data to the regression value.     for i, record := range records {         // Skip the header.         if i == 0 {             continue         }          // Parse the house price, "y".         price, err := strconv.ParseFloat(records[i][2], 64)         if err != nil {             log.Fatal(err)         }          // Parse the grade value.         grade, err := strconv.ParseFloat(record[11], 64)         if err != nil {             log.Fatal(err)         }          // Add these points to the regression value.         r.Train(regression.DataPoint(price, []float64{grade}))     }      // Train/fit the regression model.     r.Run()     // Output the trained model parameters.     fmt.Printf(" Regression Formula: %v  ", r.Formula)

После завершения исполнения получим формулу:

Regression Formula: Predicted = -1065201.67 + Grade*209786.29

5. Тестируем модель

Предполагается, что сгенерированная формула позволяет прогнозировать продажные цены на основе колонки Grade.

Протестируем формулу. Для этого возьмём созданный ранее файл testing.csv.

Хотя у нас есть тестовые данные, нам всё же нужны какие-то данные на выходе, по которым мы поймём, насколько точна формула. Для этого воспользуемся значением коэффициента детерминации.

Коэффициент детерминации говорит нам, при какой доле зависимых переменных мы сможем прогнозировать независимые переменные. В нашем случае — сколько цен на дома можно спрогнозировать на основе данных из колонки Grade.

Генерируемое значение коэффициента будет лежать в диапазоне от 0 до 1 (чем выше, тем лучше).

Вот код, генерирующий коэффициент детерминации:

func main() {         // we open the csv file from the disk         f, err := os.Open("./datasets/testing.csv")         if err != nil {                 log.Fatal(err)         }         defer f.Close()          // we create a new csv reader specifying         // the number of columns it has         salesData := csv.NewReader(f)         salesData.FieldsPerRecord = 21          // we read all the records         records, err := salesData.ReadAll()         if err != nil {                 log.Fatal(err)         }          // by slicing the records we skip the header         records = records[1:]         // Loop over the test data predicting y         observed := make([]float64, len(records))         predicted := make([]float64, len(records))         var sumObserved float64         for i, record := range records {                 // Parse the house price, "y".                 price, err := strconv.ParseFloat(records[i][2], 64)                 if err != nil {                         log.Fatal(err)                 }                 observed[i] = price                 sumObserved += price                  // Parse the grade value.                 grade, err := strconv.ParseFloat(record[11], 64)                 if err != nil {                         log.Fatal(err)                 }                  // Predict y with our trained model.                 predicted[i] = predict(grade)         }          mean := sumObserved / float64(len(observed))         var observedCoefficient, predictedCoefficient float64         for i := 0; i < len(observed); i++ {                 observedCoefficient += math.Pow((observed[i] - mean), 2)                 predictedCoefficient += math.Pow((predicted[i] - mean), 2)         }         rsquared := predictedCoefficient / observedCoefficient          // Output the R-squared to standard out.         fmt.Printf("R-squared = %0.2f  ", rsquared) }  func predict(grade float64) float64 {         return -1065201.67 + grade*209786.29 }

Обратите внимание, что функция predict — линейное уравнение, которое мы сгенерировали с помощью тестового датасета.

Вот что у нас получилось:

R-squared = 0.46

Неидеально.

Попробуем визуализировать нашу регрессию и попытаемся её улучшить.

6. Визуализируем модель

Для визуализации напишем ещё немного кода:

    // we open the csv file from the disk     f, err := os.Open("kc_house_data.csv")     if err != nil {         log.Fatal(err)     }     defer f.Close()     df := dataframe.ReadCSV(f)      // pts will hold the values for plotting.     pts := make(plotter.XYs, df.Nrow())     // ptsPred will hold the predicted values for plotting.     ptsPred := make(plotter.XYs, df.Nrow())      yVals := df.Col("price").Float()     for i, floatVal := range df.Col("grade").Float() {         pts[i].X = floatVal         pts[i].Y = yVals[i]         ptsPred[i].X = floatVal         ptsPred[i].Y = predict(floatVal)     }      // Create the plot.     p, err := plot.New()     if err != nil {         log.Fatal(err)     }     p.X.Label.Text = "grade"     p.Y.Label.Text = "house price"     p.Add(plotter.NewGrid())     // Add the scatter plot points for the observations.     s, err := plotter.NewScatter(pts)     if err != nil {         log.Fatal(err)     }     s.GlyphStyle.Radius = vg.Points(2)     s.GlyphStyle.Color = color.RGBA{R: 0, G: 0, B: 255, A: 255}     // Add the line plot points for the predictions.     l, err := plotter.NewLine(ptsPred)     if err != nil {         log.Fatal(err)     }     l.LineStyle.Width = vg.Points(0.5)     l.LineStyle.Dashes = []vg.Length{vg.Points(2), vg.Points(2)}     l.LineStyle.Color = color.RGBA{R: 255, G: 0, B: 0, A: 255}     // Save the plot to a PNG file.     p.Add(s, l)     if err := p.Save(10*vg.Centimeter, 10*vg.Centimeter, "./graphs/first_regression.png"); err != nil {         log.Fatal(err)     }

И наконец-то мы получили нашу первую линейную регрессию:

Если посмотреть внимательнее, то станет понятно, что синие кружки лучше всего укладываются на кривую линию, а не прямую.

Чтобы улучшить результат, можно попробовать заменить текущую линейную формулу параболической: y = ax + bx^2 + c.

И опять использовать колонку Grade для представления x-переменной, и новая формула будет выглядеть так:

price = a * grade + b * grade^2 + c

Обновим код обучающей функции:

    // ... everything is the same up to here     r.SetVar(1, "Grade2") // now we add one more variable, Grade^2     // ... everything is the same also here     // except we are now addin the new variable     r.Train(regression.DataPoint(price, []float64{grade, math.Pow(grade, 2)}))     // ...

Получим новую формулу:

Regression Formula: Predicted = 1639674.31 + Grade*-473161.41 + Grade2*42070.46

Теперь можно снова вычислить коэффициент детерминации:

R-squared = 0.52

Стало получше! Помните, нужно получить значение как можно ближе к 1.

Теперь обновим код, рисующий график:

    // ... we open the file etc         // pts will hold the values for plotting.     pts := make(plotter.XYs, df.Nrow())      yVals := df.Col("price").Float()     for i, floatVal := range df.Col("grade").Float() {         pts[i].X = floatVal         pts[i].Y = yVals[i]     }      // Create the plot.     p, err := plot.New()     if err != nil {         log.Fatal(err)     }     p.X.Label.Text = "grade"     p.Y.Label.Text = "house price"     p.Add(plotter.NewGrid())     // Add the scatter plot points for the observations.     s, err := plotter.NewScatter(pts)     if err != nil {         log.Fatal(err)     }     s.GlyphStyle.Radius = vg.Points(2)     s.GlyphStyle.Color = color.RGBA{R: 0, G: 0, B: 255, A: 255}      curve := plotter.NewFunction(predict)     curve.LineStyle.Width = vg.Points(3)     curve.LineStyle.Dashes = []vg.Length{vg.Points(3), vg.Points(3)}     curve.LineStyle.Color = color.RGBA{R: 255, G: 0, B: 0, A: 255}     // Save the plot to a PNG file.     p.Add(s, curve)     if err := p.Save(10*vg.Centimeter, 10*vg.Centimeter, "./graphs/second_regression.png"); err != nil {         log.Fatal(err)     }

Обновлённый график:

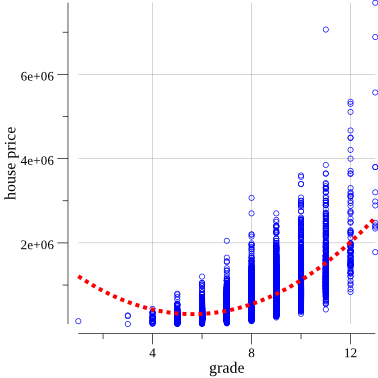
Получилось получше.

Можно сделать ещё ряд улучшений, чтобы получить значение коэффициента детерминации ближе к 1, если хотите — поэкспериментируйте. Также можно попробовать улучшить модель, изменяя или комбинируя разные переменные.

Допустим, нас устраивает формула прогнозирования, начнём её использовать. Скажем, мы хотим узнать, сколько денег можно выручить на продаже дома в категории Grade 3 в округе Кинг. Вставим значение Grade в формулу и получим цену:

598824.2200000001 USD

Надеюсь, вам было полезно это введение в использование линейно-регрессионной модели и пакетов Go, и вы теперь сможете начать осваивать машинное обучение.

Весь код из статьи лежит в репозитории.