Кластеризация графов и поиск сообществ. Часть 1: введение, обзор инструментов и Волосяные Шары
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2017-11-25 15:59
В нашей работе часто возникает потребность в выделении сообществ (кластеров) разных объектов: пользователей, сайтов, продуктовых страниц интернет-магазинов. Польза от такой информации весьма многогранна – вот лишь несколько областей практического применения качественных кластеров:

С точки зрения машинного обучения получение подобных связанных групп выглядит как типичная задача кластеризации. Однако не всегда нам бывают легко доступны фичи наблюдений, в пространстве которых можно было бы искать кластеры. Контентые или семантические фичи достаточно трудоемки в получении, как и интеграция разных источников данных, откуда эти фичи можно было бы достать. Зато у нас есть DMP под названием Facetz.DCA, где на поверхности лежат факты посещений пользователями страниц. Из них легко получить количество посещений сайтов, как каждого в отдельности, так и совместных посещений для каждой пары сайтов. Этой информации уже достаточно для построения графов веб-доменов или продуктовых страниц. Теперь задачу кластеризации можно сформулировать как задачу выделения сообществ в полученных графах.
Забегая вперед, скажу, что сообщества веб-доменов нам уже удалось применить с большой пользой в рекламных RTB-кампаниях. Классическая проблема, с которой сталкиваются трейдеры — это необходимость лавировать между точностью таргетирования и объемом сегмента. С одной стороны, грубый таргетинг по социально-демографическим признакам слишком широк и неэффективен. С другой стороны, хитрые тематические сегменты зачастую слишком узки, и изменения порогов вероятности в классификаторах не способны расширить сегмент до необходимого объема (скажем, до нескольких десятков миллионов кук). В то же время, люди, часто посещающие домены из одного кластера, образуют хорошие сегменты как раз для таких широкоохватных кампаний.
В данной серии постов я попробую остановиться больше на алгоритмической стороне задачи, чем на бизнесовой, и сделать следующее. Во-первых, описать наши эксперименты и показать картинки, которые у нас получились. Во-вторых, подробно остановиться на методах: что мы применили / хотели применить, но передумали / всё ещё хотим применить в перспективе.
Многим из вас, вероятно, приходилось кластеризовать данные, но, вероятно, большинство, как и мы, никогда не кластеризовали граф. Главная особенность кластеризации графов — это отсутствие фичей наблюдений. У нас нет расстояния между двумя произвольными точками в пространстве, потому что нет самого пространства, нет нормы, и невозможно определить расстояние. Вместо этого, у нас есть метаданные рёбер (в идеале, для каждой пары вершин). Если имеется «вес» ребра, то его можно интерпретировать как расстояние (или, наоборот, как схожесть), и тогда у нас определены расстояния для каждой пары вершин.
Многие из алгоритмов кластеризации в евклидовом пространстве подходят и для графов, так как для этих алгоритмов требуется лишь знать расстояние между наблюдениями, а не между произвольными «точками в пространстве». Некоторые требуют именно пространство фичей и для графов не годятся (например, k-means). С другой стороны, у графов есть много своих уникальных свойств, которые тоже можно использовать: компоненты связности, локальные скопления рёбер, места зацикливания информационных потоков и др.
Если цель — провести воспроизводимый эксперимент на небольших данных, а не выкатывать в продакшн готовый продукт, то среди всего вышеперечисленного лучшими вариантами являются, на наш взгляд, graph-tool (пункт 3), Gephi (пункт 4) или Infomap (пункт 9).
 и
и  — это выборочная оценка того, насколько события «посещение юзером
— это выборочная оценка того, насколько события «посещение юзером  домена
домена  » и «посещение юзером
» и «посещение юзером  домена
домена  » близки к независимости. Если
» близки к независимости. Если  — общее количество рассматриваемых юзеров, а
— общее количество рассматриваемых юзеров, а  — количество юзеров, посетивших
— количество юзеров, посетивших  , то:
, то:
 Чтобы избавиться от шумов, нужно отфильтровать домены со слишком маленьким числом посещений, а также рёбра с низким аффинити. Практика показывает, что достаточно порога в 15-20 по посещениям и 20-25 по аффинити. При более высоком пороге по аффинити в результате появляется слишком много изолированных вершин. Подобный способ построения графа позволяет увидеть в данных довольно четкую структуру «сообществ» доменов. Одна из интересных его особенностей состоит в том, что самые крупные домены (поисковики, социальные сети, некоторые крупные магазины и новостные сайты), как правило, не имеют очень «толстых» рёбер ни с одной другой вершиной. Это приводит к тому, что эти домены находятся на отшибе и часто остаются изолированными вершинами, не попадая ни в один из кластеров. Мы считаем это плюсом, так как совместное посещение vk.com и какого-нибудь узкоспециализированного сайта действительно мало что говорит о их связи друг с другом. Надо сказать, что получить и отфильтровать данные, построить граф и посчитать по нему разные матрицы — задача намного более ресурсоемкая, чем получение самих кластеров. Некоторые этапы (в частности, вычисление попарной схожести) удалось распараллелить с помощью пакета pathos (pathos.multiprocessing). В отличие от стандартного питоновского пакета multiprocessing, он не испытывает проблем с сериализацией, поскольку использует dill вместо pickle. Синтаксис у него абсолютно идентичен стандартному multiprocessing. Здесь можно почитать про dill.
Чтобы избавиться от шумов, нужно отфильтровать домены со слишком маленьким числом посещений, а также рёбра с низким аффинити. Практика показывает, что достаточно порога в 15-20 по посещениям и 20-25 по аффинити. При более высоком пороге по аффинити в результате появляется слишком много изолированных вершин. Подобный способ построения графа позволяет увидеть в данных довольно четкую структуру «сообществ» доменов. Одна из интересных его особенностей состоит в том, что самые крупные домены (поисковики, социальные сети, некоторые крупные магазины и новостные сайты), как правило, не имеют очень «толстых» рёбер ни с одной другой вершиной. Это приводит к тому, что эти домены находятся на отшибе и часто остаются изолированными вершинами, не попадая ни в один из кластеров. Мы считаем это плюсом, так как совместное посещение vk.com и какого-нибудь узкоспециализированного сайта действительно мало что говорит о их связи друг с другом. Надо сказать, что получить и отфильтровать данные, построить граф и посчитать по нему разные матрицы — задача намного более ресурсоемкая, чем получение самих кластеров. Некоторые этапы (в частности, вычисление попарной схожести) удалось распараллелить с помощью пакета pathos (pathos.multiprocessing). В отличие от стандартного питоновского пакета multiprocessing, он не испытывает проблем с сериализацией, поскольку использует dill вместо pickle. Синтаксис у него абсолютно идентичен стандартному multiprocessing. Здесь можно почитать про dill.

На картинке нарисован его разреженный вариант: большая часть рёбер удалена по методу local sparsification (он будет описан в следующей части), из-за чего группировка в сообщества выглядит более отчетливо, и смягчается эффект «Большого Волосяного Шара». Кластеров всего 18. Полный размер картинки (в png).
На каждой вершине написано название домена и номер кластера, которому он принадлежит. Обратите внимание на изолированные вершины по внешней окружности — это, как правило, крупные домены без сильных связей с кем-либо. Нижнюю часть графа можно охарактеризовать как более «женскую» (вернее, «семейную»). Она довольно беспорядочная, вероятно, потому что с одного браузера (с одной куки) страницы просматривали несколько членов семьи в разное время. С выделением сообществ в этой части графа алгоритм справился не очень хорошо.
В один огромный кластер под номером 17 (розовый) попало много чего — от сайтов по ведению беременности внизу и медицинских сайтов в центре, до мешанины из прогнозов погоды, женских форумов и журналов в верхней части кластера. К «юго-западу» от него расположен кулинарный кластер (номер 4):
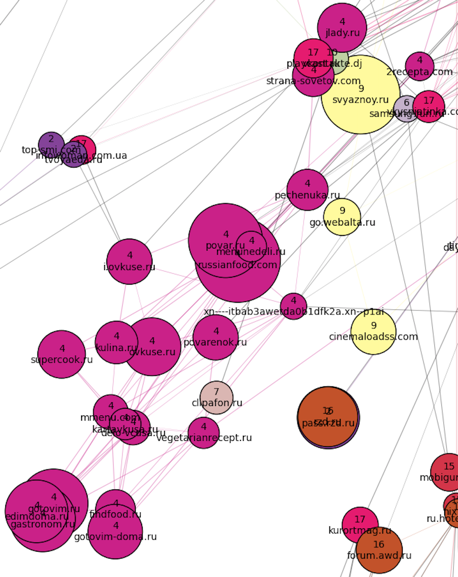 К «юго-востоку» от семейного кластера — недвижимость + поиск работы (объединились в один кластер номер 2):
К «юго-востоку» от семейного кластера — недвижимость + поиск работы (объединились в один кластер номер 2):
 К «югу» от кластера 17 расположилась очень плохо размеченная область. Так, алгоритму не удалось выделить сообщество туристических доменов (они разбросаны по разным сообществам), а в кластер кулинарии попал сайт про оружие.
К «югу» от кластера 17 расположилась очень плохо размеченная область. Так, алгоритму не удалось выделить сообщество туристических доменов (они разбросаны по разным сообществам), а в кластер кулинарии попал сайт про оружие.
В небольшой кластер 15 (красный) попали, в основном, юридические сайты:
 К «северо-западу» от «семейной» части расположены наиболее четкие кластеры. По всей видимости, браузерами посетителей этих сайтов никто больше не пользуется (и это логично, исходя из тематик кластеров). Во-первых, бросаются в глаза два плотных кластера: российские (номер 16, кирпичный) и украинские (номер 12, синий) новостные сайты, причем последний намного плотнее, хоть и меньше по размеру. Можно заметить также, что меняется ангажированность сайтов вдоль российского кластера:
К «северо-западу» от «семейной» части расположены наиболее четкие кластеры. По всей видимости, браузерами посетителей этих сайтов никто больше не пользуется (и это логично, исходя из тематик кластеров). Во-первых, бросаются в глаза два плотных кластера: российские (номер 16, кирпичный) и украинские (номер 12, синий) новостные сайты, причем последний намного плотнее, хоть и меньше по размеру. Можно заметить также, что меняется ангажированность сайтов вдоль российского кластера:
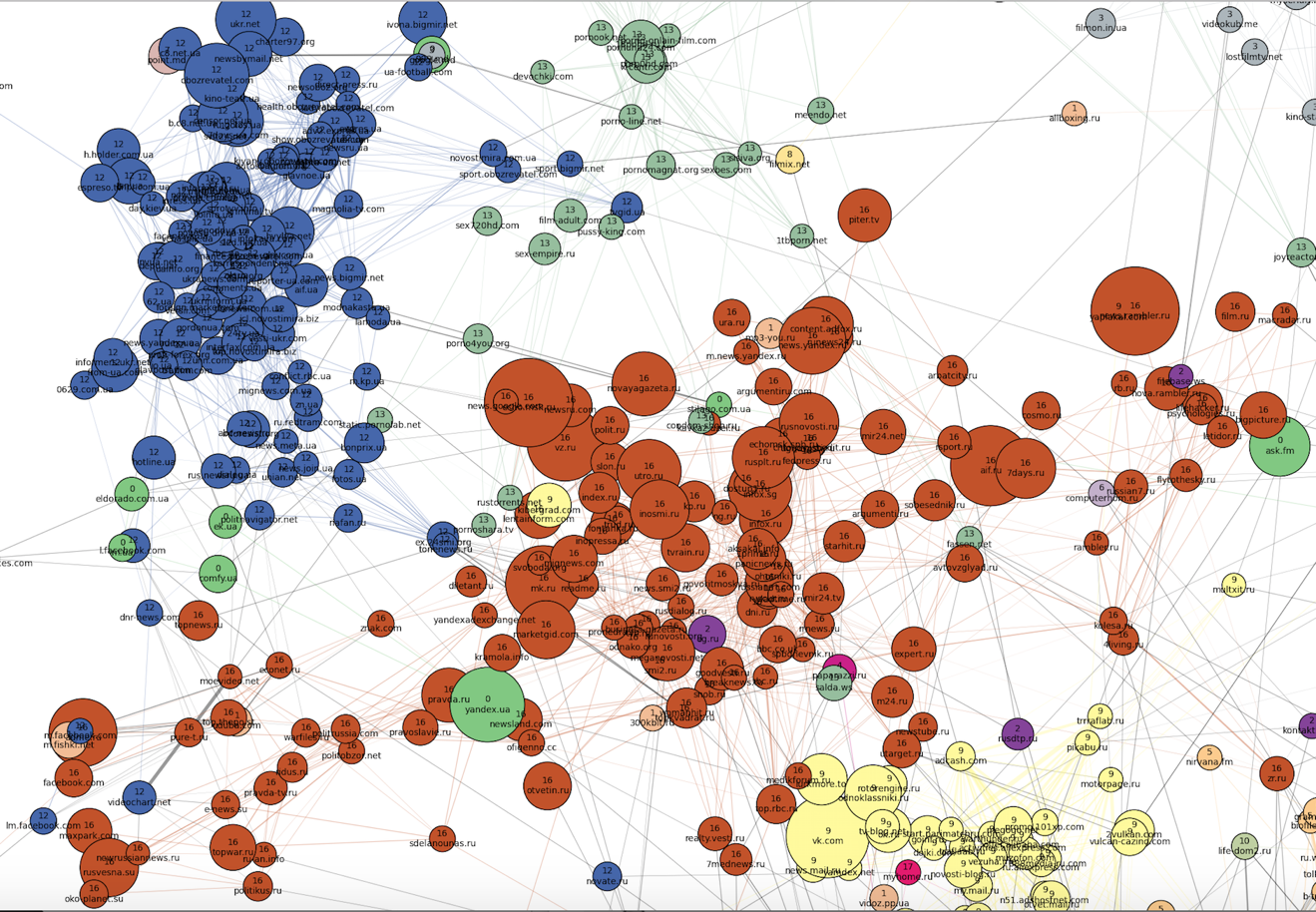 К «северо-востоку» от новостных сайтов располагаются фильмы, сериалы и онлайн-кинотеатры (серый и желтый кластеры под номерами 3 и 8). Между кластерами фильмов и кластером украинских новостей как переходная зона расположен кластер порнографии.
К «северо-востоку» от новостных сайтов располагаются фильмы, сериалы и онлайн-кинотеатры (серый и желтый кластеры под номерами 3 и 8). Между кластерами фильмов и кластером украинских новостей как переходная зона расположен кластер порнографии.
 Ещё восточнее расположен кластер номер 1 — весь казахский интернет. Рядом с ним — автомобильные сайты (кластер 6, сиреневый) и российские спортивные сайты (они влились к остальным новостям в кластер 16).
Ещё восточнее расположен кластер номер 1 — весь казахский интернет. Рядом с ним — автомобильные сайты (кластер 6, сиреневый) и российские спортивные сайты (они влились к остальным новостям в кластер 16).
 Далее к югу расположен кластер мультфильмов и детских игр (номер 10, болотный), а также тесно связанные с ним школьные кластера словарей, онлайн-решебников и рефератов: крупный российский (номер 5, персиковый) и совсем небольшой украинский (номер 0, зеленый). В кластер номер 0 также попали украинские сайты всех тематик, кроме новостей (их оказалось совсем немного). Школьные кластеры на «юге» плавно переходят в главный женский кластер номер 17.
Далее к югу расположен кластер мультфильмов и детских игр (номер 10, болотный), а также тесно связанные с ним школьные кластера словарей, онлайн-решебников и рефератов: крупный российский (номер 5, персиковый) и совсем небольшой украинский (номер 0, зеленый). В кластер номер 0 также попали украинские сайты всех тематик, кроме новостей (их оказалось совсем немного). Школьные кластеры на «юге» плавно переходят в главный женский кластер номер 17.
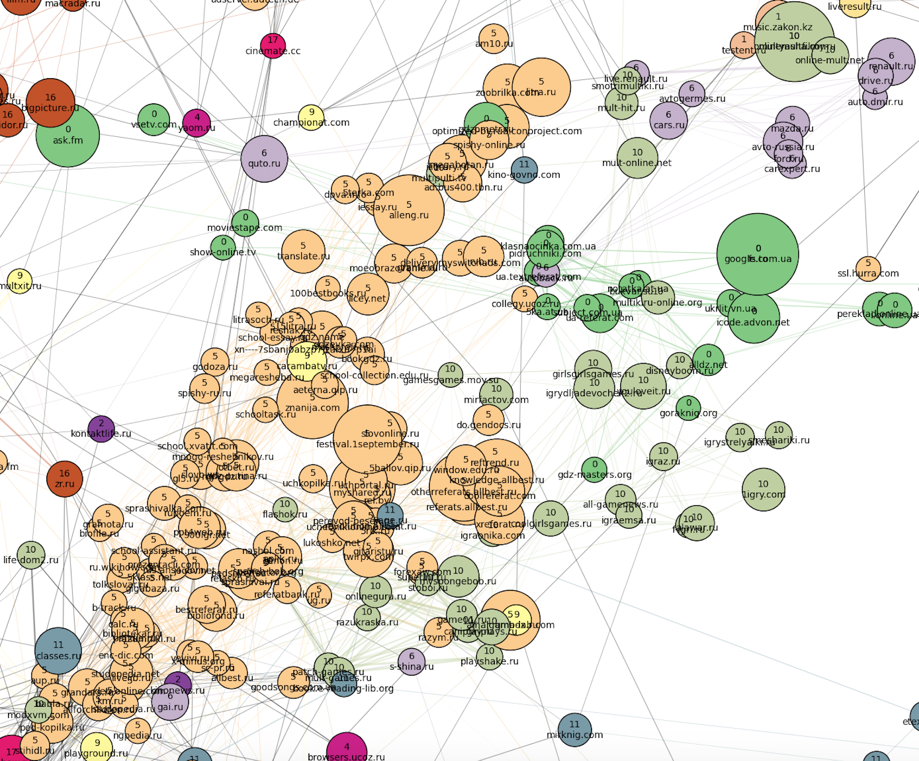 Последнее, что можно тут отметить — кластер книг, расположенный на отшибе в «восточной» части картинки:
Последнее, что можно тут отметить — кластер книг, расположенный на отшибе в «восточной» части картинки:


Полный размер.
А вот так выглядит приблизительно аналогичный граф, построенный за почти год до предыдущего. В нем 12 кластеров:
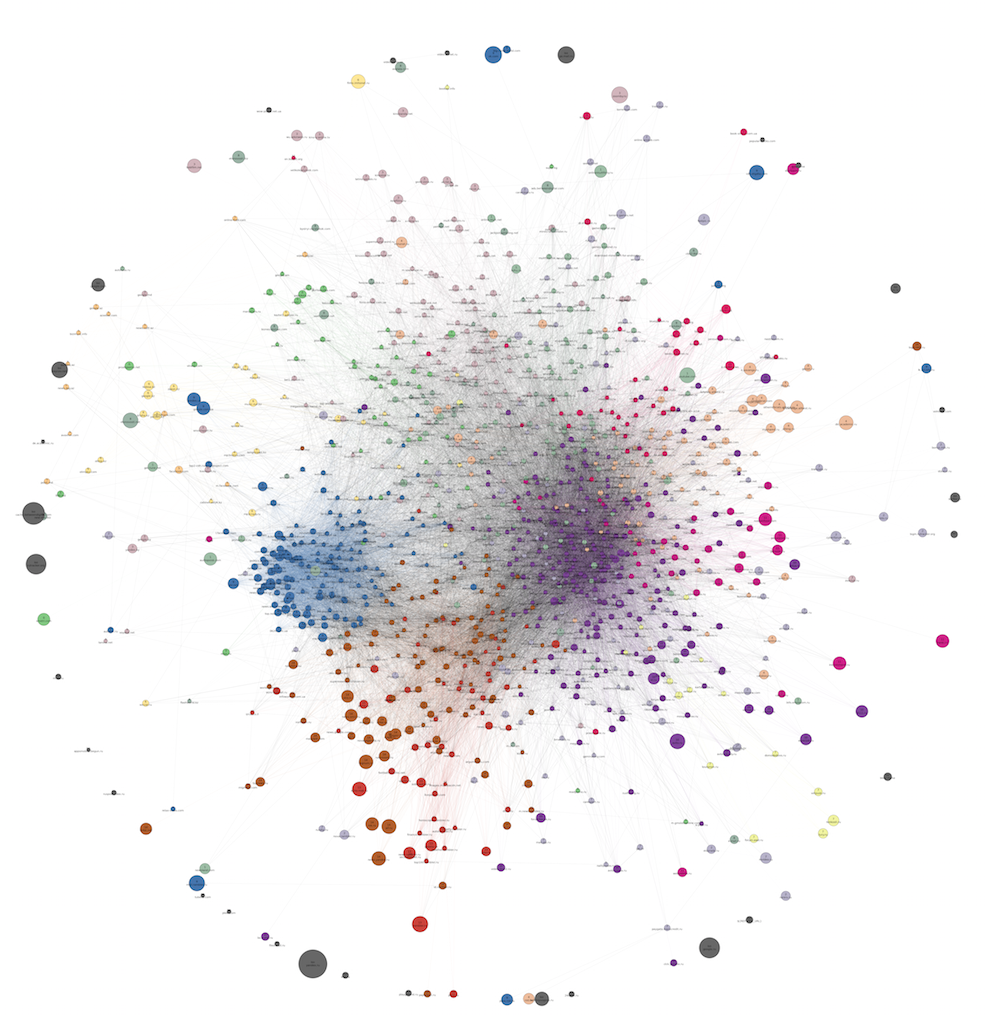
Полный размер.
Как можно заметить, за это время структура в целом осталась прежней (новостные сайты, крупный женский кластер, крупная разреженная область развлекательных сайтов разной направленности). Из различий можно отметить окончательное исчезновения кластера с музыкой за это время. Вероятно, за это время люди для нахождения музыки почти перестали пользоваться специализированными сайтами, чаще обращаясь к соцсетям и набирающим обороты сервисам вроде Spotify. Разделяемость всего графа на сообщества в целом возросла, и количество осмысленных кластеров удалось довести с 12 до 18. Причины этого, скорее всего, кроются не в изменении поведения пользователей, а просто в изменении наших источников данных и механизма сбора данных.
Если мы увеличим выборку пользователей и оставим на прежнем уровне фильтры на минимальное количество посещений домена и пары доменов, а также минимальное аффинити для формирования ребра, мы получим более крупный граф. Ниже представлен такой граф из 10121 вершины и 30 кластеров. Как видно, силовой алгоритм рисования из networkx уже не очень-то справляется и выдает довольно путаную картинку. Тем не менее, некоторые паттерны можно проследить и в таком виде. Количество рёбер уменьшено с полутора миллионов до 40000 с помощью такого же метода разрежения (local sparsification). PNG-файл занимает 80 Мб, поэтому просьба смотреть в полном размере здесь.
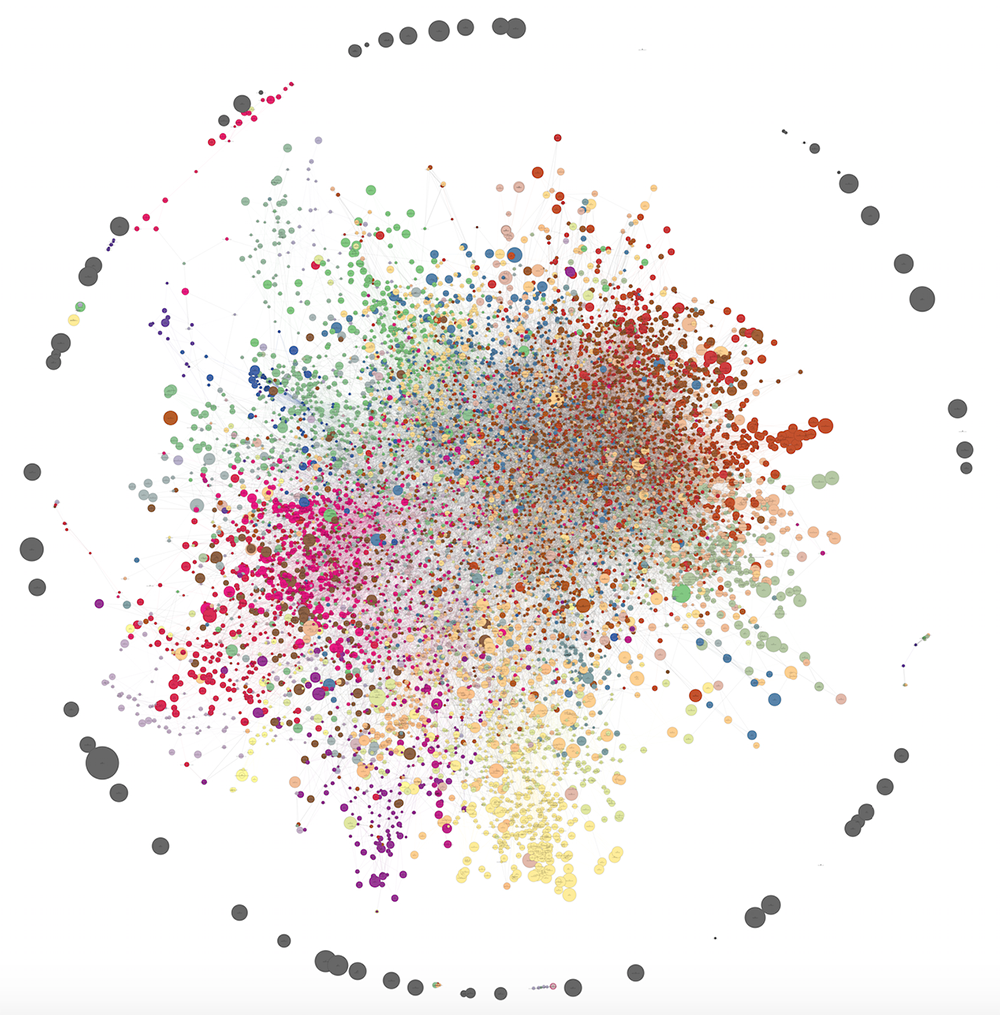 На визуализации не удалось как следует выделить структуру сообществ (мешанина в центре), но в действительности кластера получились не менее осмысленными, чем в случае 1285 доменов.
На визуализации не удалось как следует выделить структуру сообществ (мешанина в центре), но в действительности кластера получились не менее осмысленными, чем в случае 1285 доменов.
С увеличением количества данных наблюдаются интересные закономерности. С одной стороны, начинают выделяться маленькие периферийные кластера, которые были неразличимы на малых данных. С другой стороны, то, что плохо кластеризовалось на малых данных, плохо кластеризуется и на больших (например, смешиваются сайты про недвижимость и про поиск работы, часто к ним примыкает эзотерика и астрология).
Вот несколько примеров новых сообществ. На самом отшибе выделился испанский кластер, так как мы что-то видим оттуда:
 Недалеко от него, ближе к основному скоплению точек, располагается азербайджанский кластер (номер 2) и грузинский (номер 4):
Недалеко от него, ближе к основному скоплению точек, располагается азербайджанский кластер (номер 2) и грузинский (номер 4):
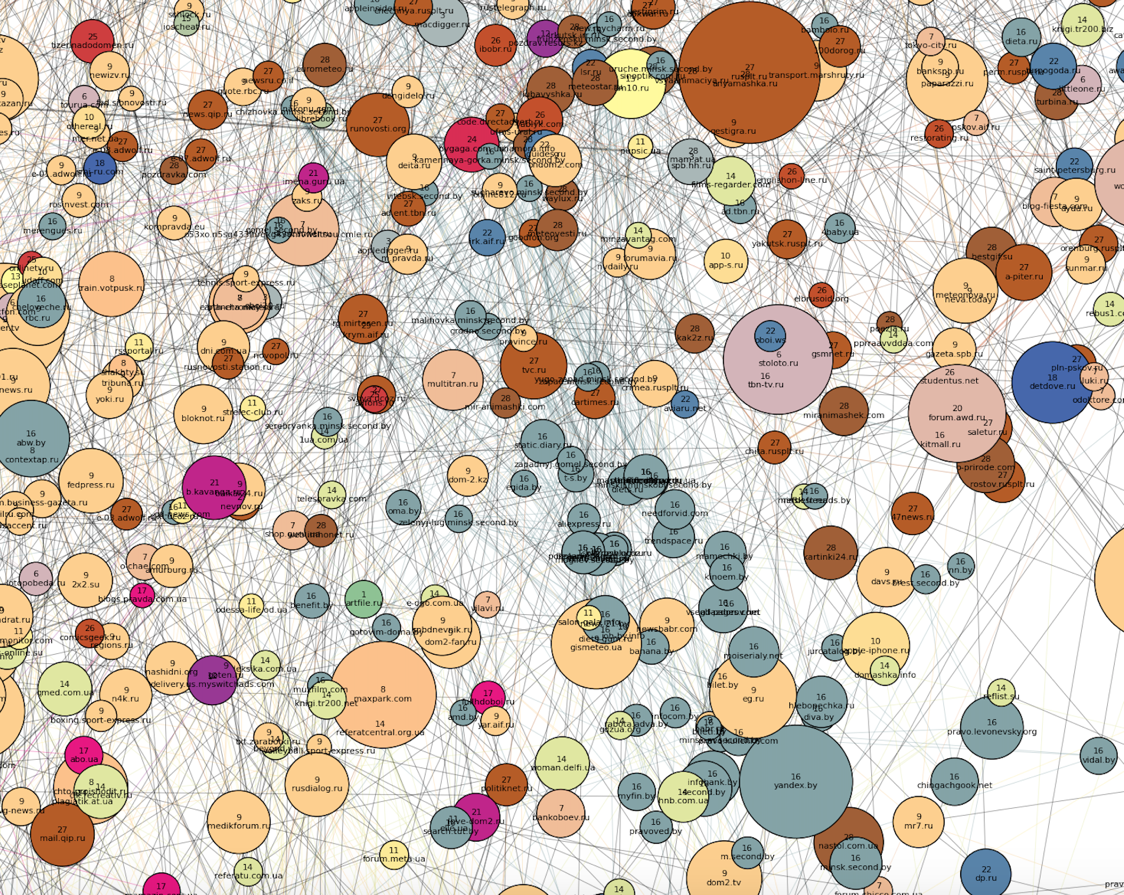
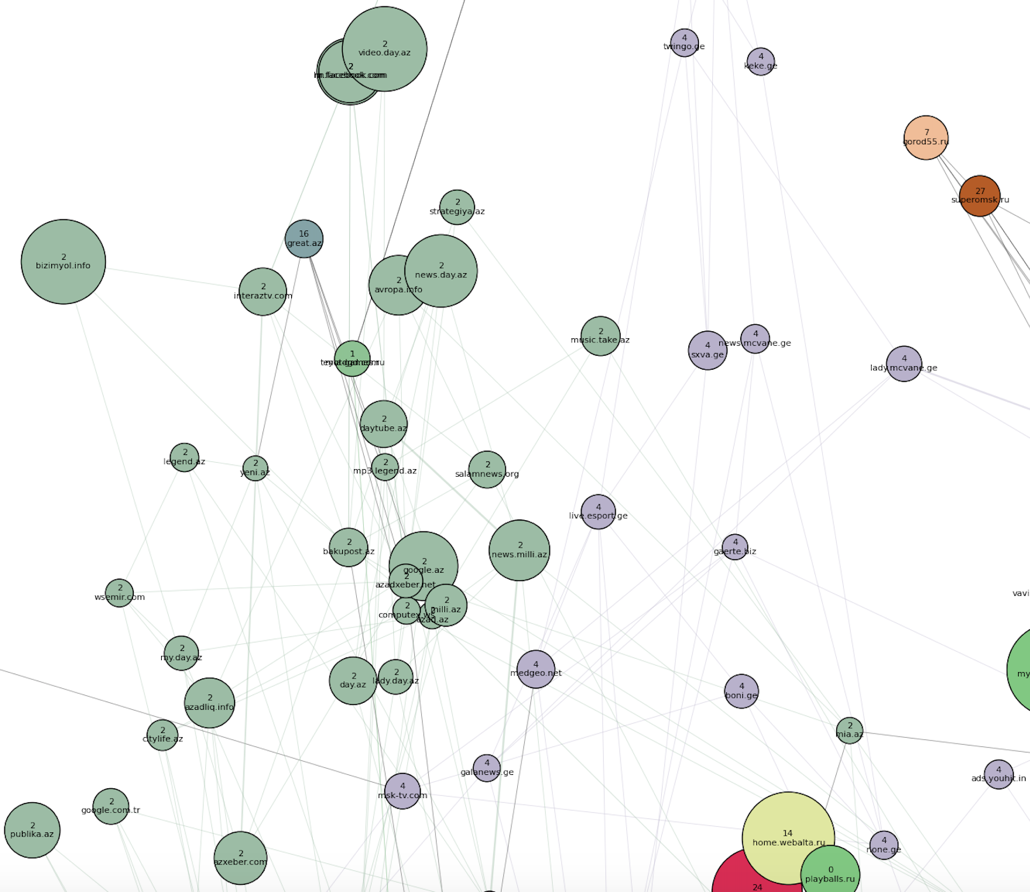 Появился узбекско-таджикский кластер, а также белорусский (номер 16) — внутри основной массы доменов, рядом с «российским новостным» и «украинским неновостным» сообществами:
Появился узбекско-таджикский кластер, а также белорусский (номер 16) — внутри основной массы доменов, рядом с «российским новостным» и «украинским неновостным» сообществами:
 В следующем посте будет описание алгоритма:
В следующем посте будет описание алгоритма:
– как были получены сами кластера, чтобы можно было так раскрашивать граф;
– как удалялись избыточные рёбра.
Готовы ответить на ваши вопросы в комментариях. Stay tuned!
- Выделение сегментов пользователей для проведения таргетированных рекламных кампаний.
- Использование кластеров в качестве предикторов («фичей») в персональных рекомендациях (в content-based методах или как дополнительная информация в коллаборативной фильтрации).
- Снижение размерности в любой задаче машинного обучения, где в качестве фичей выступают страницы или домены, посещенные пользователем.
- Сличение товарных URL между различными интернет-магазинами с целью выявления среди них групп, соответствующих одному и тому же товару.
- Компактная визуализация — человеку будет проще воспринимать структуру данных.

С точки зрения машинного обучения получение подобных связанных групп выглядит как типичная задача кластеризации. Однако не всегда нам бывают легко доступны фичи наблюдений, в пространстве которых можно было бы искать кластеры. Контентые или семантические фичи достаточно трудоемки в получении, как и интеграция разных источников данных, откуда эти фичи можно было бы достать. Зато у нас есть DMP под названием Facetz.DCA, где на поверхности лежат факты посещений пользователями страниц. Из них легко получить количество посещений сайтов, как каждого в отдельности, так и совместных посещений для каждой пары сайтов. Этой информации уже достаточно для построения графов веб-доменов или продуктовых страниц. Теперь задачу кластеризации можно сформулировать как задачу выделения сообществ в полученных графах.
Забегая вперед, скажу, что сообщества веб-доменов нам уже удалось применить с большой пользой в рекламных RTB-кампаниях. Классическая проблема, с которой сталкиваются трейдеры — это необходимость лавировать между точностью таргетирования и объемом сегмента. С одной стороны, грубый таргетинг по социально-демографическим признакам слишком широк и неэффективен. С другой стороны, хитрые тематические сегменты зачастую слишком узки, и изменения порогов вероятности в классификаторах не способны расширить сегмент до необходимого объема (скажем, до нескольких десятков миллионов кук). В то же время, люди, часто посещающие домены из одного кластера, образуют хорошие сегменты как раз для таких широкоохватных кампаний.
В данной серии постов я попробую остановиться больше на алгоритмической стороне задачи, чем на бизнесовой, и сделать следующее. Во-первых, описать наши эксперименты и показать картинки, которые у нас получились. Во-вторых, подробно остановиться на методах: что мы применили / хотели применить, но передумали / всё ещё хотим применить в перспективе.
Многим из вас, вероятно, приходилось кластеризовать данные, но, вероятно, большинство, как и мы, никогда не кластеризовали граф. Главная особенность кластеризации графов — это отсутствие фичей наблюдений. У нас нет расстояния между двумя произвольными точками в пространстве, потому что нет самого пространства, нет нормы, и невозможно определить расстояние. Вместо этого, у нас есть метаданные рёбер (в идеале, для каждой пары вершин). Если имеется «вес» ребра, то его можно интерпретировать как расстояние (или, наоборот, как схожесть), и тогда у нас определены расстояния для каждой пары вершин.
Многие из алгоритмов кластеризации в евклидовом пространстве подходят и для графов, так как для этих алгоритмов требуется лишь знать расстояние между наблюдениями, а не между произвольными «точками в пространстве». Некоторые требуют именно пространство фичей и для графов не годятся (например, k-means). С другой стороны, у графов есть много своих уникальных свойств, которые тоже можно использовать: компоненты связности, локальные скопления рёбер, места зацикливания информационных потоков и др.
Обзор инструментов
К настоящему моменту люди изобрели огромное количество методов кластеризации графов — каждый со своими преимуществами и косяками. В одном из следующих постов разберем подробнее некоторые алгоритмы и их свойства. А пока считаем полезным поделиться ссылками на открытые инструменты для анализа графов, где уже реализовано что-то для кластеризации и нахождения сообществ.- Очень модный и развивающийся нынче GraphX. Его нужно было написать первым элементом в списке, но как таковых готовых алгоритмов кластеризации там пока нет (версия 1.4.1). Есть подсчет треугольников и связных компонент, что, вкупе с стандартными операциями над Spark RDD, можно использовать для написания своих алгоритмов. Пока что у GraphX есть апи только для scala, что также может усложнить его использование.
- Библиотека для Apache Giraph под названием Okapi использует несколько алгоритмов, в том числе достаточно новый алгоритм собственной разработки под названием Spinner, основанный на label propagation. Giraph — это надстройка над Hadoop, предназначенная для обработки графов. В ней почти нет машинного обучения, и для компенсации этого в компании Telefonica и был создан Okapi. Вероятно, сейчас Giraph выглядит уже не так перспективно на фоне GraphX, но сам алгоритм Spinner хорошо ложится и на парадигму Spark. Про Spinner можно прочитать здесь.
- Библиотека graph-tool для питона содержит несколько новейших алгоритмов кластеризации и очень быстро работает. Мы использовали её для сличения URL, соответствующих одному и тому же товару. Все, что можно, распараллелено по ядрам процессора, и для локальных вычислений (графы размером до пары сотен тысяч узлов) это самый быстрый вариант.
- Gephi — известный инструмент, который мы обошли вниманием, возможно, незаслуженно. Долгое время Gephi практически не развивался, зато у него появились хорошие плагины, в том числе для выделения сообществ. В последнее время проект вновь ожил и ожидается версия 0.9
- GraphLab Create. Это питоновская обертка над C++, позволяющая прогонять машинное обучение как локально, так и распределенно (на Yarn). Кластеризации графов там все ещё нет, только нахождение k-ядер.
- Хваленый networkX, несмотря на обилие алгоритмов, не умеет кластеризовать графы, но только анализировать связные компоненты и клики. Вдобавок он намного медленнее graph-tool, и по части визуализации уступает тому же graph-tool и gephi.
- Реализация алгоритма марковской кластеризации (MCL) от его изобретателя. Автор снизил сложность обычного MCL в худшем случае с
до
, где
— число узлов, а
— максимальная степень узла, и обижается, когда алгоритм MCL называют немасштабируемым.Также он добавил фишки для регулировки числа кластеров. Однако у MCL было несколько других серьезных проблем, и непонятно, решены ли они. Например, проблема нестабильности размера кластеров (наш небольшой эксперимент выдал одну гигантскую связную компоненту и много маленьких кластерочков по 2-3 узла, но, возможно, мы не нашли нужную ручку). Последняя новость на сайте датируется 2012 годом, что не очень хорошо.
- Разные реализации одного из самых популярных алгоритмов Louvain: для C, для Python, ещё для Python. Классическая статья про этот алгоритм: ссылка.
- Сайт, посвященный алгоритму Infomap и его модификациям, от авторов метода. Как и везде, есть открытый код. Помимо хорошей поддержки и документации, есть изумительные демки, иллюстрирующие работу алгоритма: вот и вот. Узнать, как работает алгоритм, можно здесь.
- Пакет для R под названием igraph. В нем реализовано довольно много алгоритмов кластеризации, но мы не можем сказать ничего конкретного о них, поскольку не изучали пакет.
Если цель — провести воспроизводимый эксперимент на небольших данных, а не выкатывать в продакшн готовый продукт, то среди всего вышеперечисленного лучшими вариантами являются, на наш взгляд, graph-tool (пункт 3), Gephi (пункт 4) или Infomap (пункт 9).
Наши эксперименты
А теперь мы расскажем, как мы формировали графы доменов Рунета и окрестностей, и покажем картинки с результатами их кластеризации. В следующей части нашего цикла статей будет описан алгоритм, с помощью которого были получены приведенные ниже картинки. Это модифицированный k-medoids, который мы в лучших традициях велосипедирования написали на корневом питоне, и с помощью которого удалось на удивление хорошо решить некоторые задачи. Часть информации из этого и следующего поста, а также описание некоторых других алгоритмов, есть в презентации, которую я рассказывал на newprolab в digital october этой весной:Данные
Первая задача — кластеризация веб-доменов. Из DMP мы берем данные о посещениях пользователями различных доменов, и на их основе строим граф, где в качестве узлов выступают домены, а в качестве рёбер — аффинити между доменами. Аффинити (он же лифт) между доменамиВизуализация
Пришло время показать немного картинок с графами (как они получились, мы расскажем в следующей части). Известно, что networkX не предназначен для визуализации графов, и что для этой цели лучше обращаться к d3.js, gephi или graph-tool. Мы слишком поздно узнали об этом, и вопреки здравому смыслу, все равно продолжили мужественно рисовать картинки в networkX. Получился не то чтобы чистый мёд (в частности, не удалось настроить взаимное отталкивание узлов и неперекрывающиеся надписи), но мы как могли старались и выжали все что можно из возможностей networkX. Во всех картинках диаметр кружочка (домена) соответствует его посещаемости, толщина ребра соответствует аффинити, цвет кружочка означает принадлежность домена кластеру. Цвет ребра означает принадлежность обеих вершин данному кластеру, серый цвет соответствует рёбрам, соединяющим вершины из разных кластеров.Комментарии к кластерам на примере одного из графов
Не очень большой граф из 1285 доменов:
На картинке нарисован его разреженный вариант: большая часть рёбер удалена по методу local sparsification (он будет описан в следующей части), из-за чего группировка в сообщества выглядит более отчетливо, и смягчается эффект «Большого Волосяного Шара». Кластеров всего 18. Полный размер картинки (в png).
На каждой вершине написано название домена и номер кластера, которому он принадлежит. Обратите внимание на изолированные вершины по внешней окружности — это, как правило, крупные домены без сильных связей с кем-либо. Нижнюю часть графа можно охарактеризовать как более «женскую» (вернее, «семейную»). Она довольно беспорядочная, вероятно, потому что с одного браузера (с одной куки) страницы просматривали несколько членов семьи в разное время. С выделением сообществ в этой части графа алгоритм справился не очень хорошо.
В один огромный кластер под номером 17 (розовый) попало много чего — от сайтов по ведению беременности внизу и медицинских сайтов в центре, до мешанины из прогнозов погоды, женских форумов и журналов в верхней части кластера. К «юго-западу» от него расположен кулинарный кластер (номер 4):
 К «юго-востоку» от семейного кластера — недвижимость + поиск работы (объединились в один кластер номер 2):
К «юго-востоку» от семейного кластера — недвижимость + поиск работы (объединились в один кластер номер 2): К «югу» от кластера 17 расположилась очень плохо размеченная область. Так, алгоритму не удалось выделить сообщество туристических доменов (они разбросаны по разным сообществам), а в кластер кулинарии попал сайт про оружие.
К «югу» от кластера 17 расположилась очень плохо размеченная область. Так, алгоритму не удалось выделить сообщество туристических доменов (они разбросаны по разным сообществам), а в кластер кулинарии попал сайт про оружие.В небольшой кластер 15 (красный) попали, в основном, юридические сайты:
 К «северо-западу» от «семейной» части расположены наиболее четкие кластеры. По всей видимости, браузерами посетителей этих сайтов никто больше не пользуется (и это логично, исходя из тематик кластеров). Во-первых, бросаются в глаза два плотных кластера: российские (номер 16, кирпичный) и украинские (номер 12, синий) новостные сайты, причем последний намного плотнее, хоть и меньше по размеру. Можно заметить также, что меняется ангажированность сайтов вдоль российского кластера:
К «северо-западу» от «семейной» части расположены наиболее четкие кластеры. По всей видимости, браузерами посетителей этих сайтов никто больше не пользуется (и это логично, исходя из тематик кластеров). Во-первых, бросаются в глаза два плотных кластера: российские (номер 16, кирпичный) и украинские (номер 12, синий) новостные сайты, причем последний намного плотнее, хоть и меньше по размеру. Можно заметить также, что меняется ангажированность сайтов вдоль российского кластера: К «северо-востоку» от новостных сайтов располагаются фильмы, сериалы и онлайн-кинотеатры (серый и желтый кластеры под номерами 3 и 8). Между кластерами фильмов и кластером украинских новостей как переходная зона расположен кластер порнографии.
К «северо-востоку» от новостных сайтов располагаются фильмы, сериалы и онлайн-кинотеатры (серый и желтый кластеры под номерами 3 и 8). Между кластерами фильмов и кластером украинских новостей как переходная зона расположен кластер порнографии. Ещё восточнее расположен кластер номер 1 — весь казахский интернет. Рядом с ним — автомобильные сайты (кластер 6, сиреневый) и российские спортивные сайты (они влились к остальным новостям в кластер 16).
Ещё восточнее расположен кластер номер 1 — весь казахский интернет. Рядом с ним — автомобильные сайты (кластер 6, сиреневый) и российские спортивные сайты (они влились к остальным новостям в кластер 16). Далее к югу расположен кластер мультфильмов и детских игр (номер 10, болотный), а также тесно связанные с ним школьные кластера словарей, онлайн-решебников и рефератов: крупный российский (номер 5, персиковый) и совсем небольшой украинский (номер 0, зеленый). В кластер номер 0 также попали украинские сайты всех тематик, кроме новостей (их оказалось совсем немного). Школьные кластеры на «юге» плавно переходят в главный женский кластер номер 17.
Далее к югу расположен кластер мультфильмов и детских игр (номер 10, болотный), а также тесно связанные с ним школьные кластера словарей, онлайн-решебников и рефератов: крупный российский (номер 5, персиковый) и совсем небольшой украинский (номер 0, зеленый). В кластер номер 0 также попали украинские сайты всех тематик, кроме новостей (их оказалось совсем немного). Школьные кластеры на «юге» плавно переходят в главный женский кластер номер 17. Последнее, что можно тут отметить — кластер книг, расположенный на отшибе в «восточной» части картинки:
Последнее, что можно тут отметить — кластер книг, расположенный на отшибе в «восточной» части картинки:
Изменения за год
Вот так выглядит тот же самый граф, только нарисованный без прореживания:
Полный размер.
А вот так выглядит приблизительно аналогичный граф, построенный за почти год до предыдущего. В нем 12 кластеров:

Полный размер.
Как можно заметить, за это время структура в целом осталась прежней (новостные сайты, крупный женский кластер, крупная разреженная область развлекательных сайтов разной направленности). Из различий можно отметить окончательное исчезновения кластера с музыкой за это время. Вероятно, за это время люди для нахождения музыки почти перестали пользоваться специализированными сайтами, чаще обращаясь к соцсетям и набирающим обороты сервисам вроде Spotify. Разделяемость всего графа на сообщества в целом возросла, и количество осмысленных кластеров удалось довести с 12 до 18. Причины этого, скорее всего, кроются не в изменении поведения пользователей, а просто в изменении наших источников данных и механизма сбора данных.
Если мы увеличим выборку пользователей и оставим на прежнем уровне фильтры на минимальное количество посещений домена и пары доменов, а также минимальное аффинити для формирования ребра, мы получим более крупный граф. Ниже представлен такой граф из 10121 вершины и 30 кластеров. Как видно, силовой алгоритм рисования из networkx уже не очень-то справляется и выдает довольно путаную картинку. Тем не менее, некоторые паттерны можно проследить и в таком виде. Количество рёбер уменьшено с полутора миллионов до 40000 с помощью такого же метода разрежения (local sparsification). PNG-файл занимает 80 Мб, поэтому просьба смотреть в полном размере здесь.
 На визуализации не удалось как следует выделить структуру сообществ (мешанина в центре), но в действительности кластера получились не менее осмысленными, чем в случае 1285 доменов.
На визуализации не удалось как следует выделить структуру сообществ (мешанина в центре), но в действительности кластера получились не менее осмысленными, чем в случае 1285 доменов.С увеличением количества данных наблюдаются интересные закономерности. С одной стороны, начинают выделяться маленькие периферийные кластера, которые были неразличимы на малых данных. С другой стороны, то, что плохо кластеризовалось на малых данных, плохо кластеризуется и на больших (например, смешиваются сайты про недвижимость и про поиск работы, часто к ним примыкает эзотерика и астрология).
Вот несколько примеров новых сообществ. На самом отшибе выделился испанский кластер, так как мы что-то видим оттуда:
 Недалеко от него, ближе к основному скоплению точек, располагается азербайджанский кластер (номер 2) и грузинский (номер 4):
Недалеко от него, ближе к основному скоплению точек, располагается азербайджанский кластер (номер 2) и грузинский (номер 4): Появился узбекско-таджикский кластер, а также белорусский (номер 16) — внутри основной массы доменов, рядом с «российским новостным» и «украинским неновостным» сообществами:
Появился узбекско-таджикский кластер, а также белорусский (номер 16) — внутри основной массы доменов, рядом с «российским новостным» и «украинским неновостным» сообществами: В следующем посте будет описание алгоритма:
В следующем посте будет описание алгоритма: – как были получены сами кластера, чтобы можно было так раскрашивать граф;
– как удалялись избыточные рёбра.
Готовы ответить на ваши вопросы в комментариях. Stay tuned!
Источник: habrahabr.ru