Нестандартная кластеризация, часть 3: приёмы и метрики для кластеризации временных рядов

Пока другие специалисты по машинному обучению и анализу данных выясняют, как прикрутить побольше слоёв к нейронной сети, чтобы она ещё лучше играла в Марио, давайте обратимся к чему-нибудь более приземлённому и применимому на практике.

Кластеризация временных рядов — неблагодарное дело. Даже при группировке статических данных часто получаются сомнительные результаты, что уж говорить про информацию, рассеянную во времени. Однако нельзя игнорировать задачу, только потому что она сложна. Попробуем разобраться, как выжать из рядов без меток немного смысла. В этой статье рассматриваются подтипы кластеризации временных рядов, общие приёмы и популярные меры расстояния между рядами. Статья рассчитана на читателя, уже имевшего дело с последовательностями в data science: о базовых вещах (тренд, ARMA/ARIMA, спектральный анализ) рассказываться не будет.

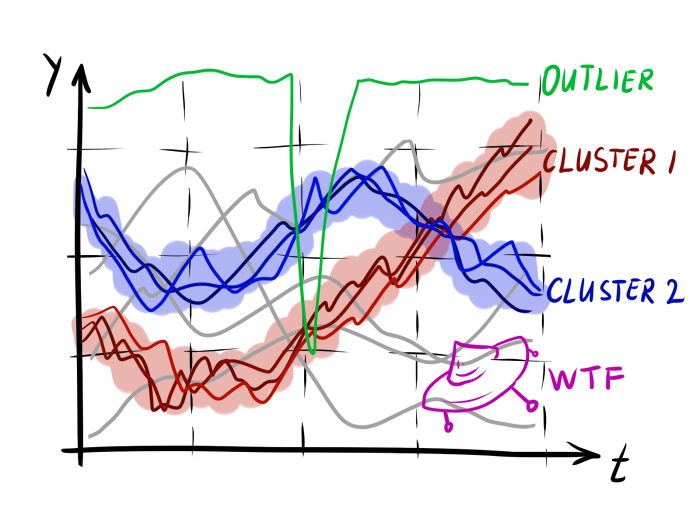
Здесь и далее $$ — временные ряды со временными отсчётами $$ и уровнями $$, $$ и $$ соответственно. Значения временных рядов — $$ — одномерные вещественные переменные. Переменная $$ считается временем, но рассмотренные ниже математические абстракции, как правило, применимы и к пространственным рядам (развёрнутая кривая), к сериям символов и последовательностям других видов (скажем, график эмоциональной окрашенности текста). $$ — функция, измеряющая насколько $$ отличается от $$. Проще всего думать о ней, как о расстоянии от $$ до $$, однако следует помнить, что она не всегда отвечает математическому определению метрики.

Подтипы «похожести» временных рядов

При работе со временными рядами встречаются многие типичные трудности data science: высокая размерность входных данных, пропущенные данные, коррелированный шум. Однако в задаче кластеризации последовательностей есть пара дополнительных трудностей. Во-первых, в рядах может быть разное количество отсчётов. Во-вторых, при работе с последовательными данными, у нас больше степеней свободы в определении того, насколько один элемент похож на другой. Дело тут не только в количестве переменных в экземпляре датасета; сам способ изменения данных во времени, тоже вносит вклад. Это очевидный, но важный момент: мы можем независимо преобразовывать или перенумеровывать значения экземпляров статических данных, но с последовательностями такое не пройдёт. Следовательно, метрики и алгоритмы должны принимать во внимание локальную зависимость данных.



Кроме того, при кластеризации рядов более сильный вклад вносит семантика данных. Например, как распределить 8 графиков на картинке на группы?



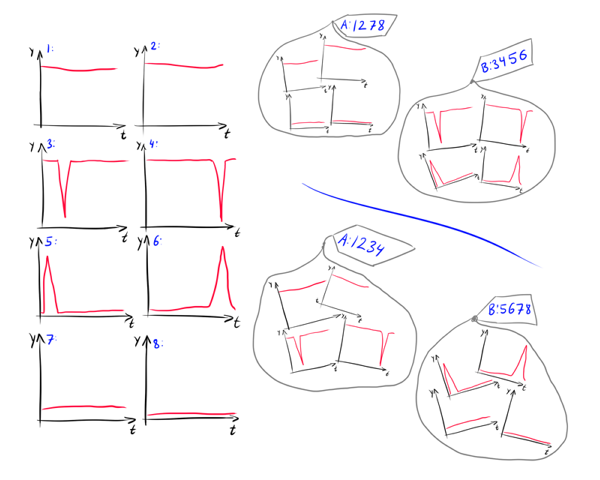
Что здесь более важно для исследователя? Средний уровень $$ или наличие скачков? Если сам $$, то первое разбиение 1234/5678 подходит лучше, если его изменения, то лучшим окажется 1278/3456. Более того, важно ли, когда именно происходит скачок? Может стоит разбить группу 3456 на подгруппы 34 и 56? В зависимости от того, что именно есть $$, на эти вопросы можно дать разные ответы.

Поэтому в связи с возможными семантическими отличями данных полезно выделять несколько типов подобия, которые могут встречаться в практических задачах[1]

• Ряды похожие во времени. Самый простой тип подобия. Мы ищем ряды, где особые точки и интервалы возрастания точно или почти точно соответствуют друг другу во времени. При этом, не обязательно, чтобы значения экстремумов и наклоны кривых точно друг с другом совпадали, лишь бы были близки в среднем. Такой тип подобия возникает, например, в задачах анализа рынка, когда мы хотим обнаружить кластеры компаний, акции которых падают и возрастают вместе. На представленном ниже рисунке графики 1 и 2 похожи во времени.
• Ряды похожие по форме. Мы ищем ряды имеющие одинаковые характерные особенности, но не налагающиеся друг на друга. Они могут быть как просто разнесены по времени, так и растянуты или ещё как-то преобразованы. Такой тип подобия встречается, например, при кластеризации звуковых сэмплов — невозможно произнести одну и ту же фразу в абсолютно одинаковом темпе. Графики 3 и 4 на рисунке похожи по форме.
• Ряды похожие по структуре. Поиск последовательностей с одинаковыми законами изменения; как глобальными — периодичность (5 и 6), тренд (7 и 8) — так и локальнами, например, сколько раз в последовательности встречается определённый паттерн.

Чёткое понимание, какой тип подобия характерен для вашей задачи — неотъемлемая часть в создании осмысленных кластеров.

Приёмы по представлению данных

Большое количество входных данных наводит на мысль о feature engineering. Лучший способ кластеризовать временные ряды — кластеризовать их НЕ как временные ряды. Если специфика задачи позволяет вам преобразовать отсчёты в данные фиксированного размера, стоит воспользоваться этой возможностью. Сразу пропадает целая группа проблем.

• Наилучший случай — когда заранее известна математическая модель, которой отвечают данные (например, дано, что последовательность представляет собой сумму конечного набора функций и шума, или известна порождающая модель). Тогда стоит перевести последовательности в пространство параметров модели, и кластеризировать уже в нём[17]. К сожалению, такое счастье выпадает редко.
• Стоит посмотреть, насколько хороший результат можно получить, собрав по датасету простые статистические показатели:
  
  
  • минимум, максимум, средний и медианный элементы (после сглаживания)
  • количество пиков и впадин
  • дисперсия элементов
  • площадь под графиком (до нормализации и вычитания среднего, если есть желание их провести)
  • сумма квадратов производной
  • показатель тренда
  • коэффициенты ARIMA, если применимо[2]
  • количество пересечений отметок в 25-ый, 50-ый, 75-ый перцентиль, пересечений среднего и нуля
  
  Даже если кластеризация одних лишь статистических сводок по рядам не даст хороших результатов, попробуйте прикрепить эти глобальные параметры к исходным данным. Это поможет разделять ряды с подобием по структуре.
• Можно попытаться применить подход bag of features. Характерные формы можно как задать и найти вручную, так и определить автоматически при помощи автоэнкодера. Вообще, подходы, основанные на кластеризации подпоследовательностей пережили в недавнем времени взлёт и падение популярности. Было показано, что слишком часто они производят бессмысленные результаты. Но если вы точно уверены что ряды из датасета имеют какие-то характерные подпоследовательности, дерзайте[3].
• Если не хочется возиться с частотной областью, но тем не менее, мысль кластеризировать ряды исходя из цикличных особенностей кажется здравой, попробуйте преобразовать ряд в автокорреляционную область и группировать данные уже в ней.

Если совсем не получается избавиться от временной зависимости, то следует попробовать хотя бы упростить ряд или перевести его в другую область:

• Если данные шумные или имеют очень большую размерность, то стоит их проредить. Воспользуйтесь вашим любимым методом поинтервальной интерполяции (самое простое — линейное приближение, Piecewise Linear Approximation, PLA, или поинтервальная интерполяция сплайнами) или алгоритмом поиском особых точек (Perceptually Important Points, PIP).
• В случае очень шумных данных также можно построить верхнюю и нижнюю огибающую для каждой временной последовательности, и кластеризовать уже получившиеся пары. Вместо одного ряда получается два, что совсем не выглядит как упрощение, но будучи применённым по назначению, такой подход делает данные более понятными как для человека, так и для компьютера[4].
• В биоинформатике и обработке символьных последовательности часто бывает полезно применить к ряду кодирование символами (Symbolic Approximation, SAX).
• Частотные показатели. Дискретное преобразование Фурье, вейвлет-преобразование, косинусное преобразование. Это не самый лучший вариант, так как мы от одной последовательности переходим к другой, часто ещё более непонятной, но иногда может помочь. Кстати, если преобразование Фурье настолько хорошо помогает, возможно, стоит воспользоваться и другими инструментами цифровой обработки сигналов.

Метрики

Вышеописанные глобальные характеристики позволят вам разделить ряды на группы похожих по структуре. Когда одно это не даёт значимых результатов, следует выбрать подобающую метрику на пространстве последовательностей. Чтобы выделить в информации ясные закономерности, нужно сконструировать хорошую функцию близости, но чтобы это сделать, надо уже иметь некоторое представление об имеющемся датасете, так что не зацикливайтесь на каком-то одном из вариантов, представленных ниже.

• Евклидово или $$-расстояние. Эти любимые всеми метрики работают только в случае поиска рядов похожих во времени. Да и в этом случае, они могут выдавать сомнительные результаты, если последовательности длинные или шумные. Но раз в год и shuffle sort стреляет.
  
  Тривиальным улучшением $$/$$-метрики является её ограничение сверху, мягкое или жёсткое: создание максимального порога для вклада разницы между уровнями отсчётов с одним $$. Применяйте его, если ожидаете, что одинарные отсчёты-выбросы могут испортить массив расстояний.
  
  Пример жёсткого ограничения:
  

  $$

  Пример мягкого ограничения (вблизи нуля функция ведёт себя как $$, но при большой разнице между $$ и $$ выходит на уровень):
  

  $$

  Здесь и далее, если метрику нельзя напрямую применить к рядам разной длины, попробуйте либо растянуть меньший ряд до размеров большего, либо протянуть его сквозь больший (на манер кросс-корреляции) и взяв наименьшее расстояние.
• Минимальная прыжковая стоимость (Minimum Jump Cost, MJC)[5]. Интересная функция непохожести, имеющая простой интуитивный смысл. Мы ставим графики вровень друг к другу, после чего двигаемся слева направо, перепрыгивая с одного графика на ближайшую (в некотором смысле) точку другого и обратно. При этом накладывается ограничение, что можно выбирать только точки, находящиеся вперёд по времени. Длина проделанного пути и будет представлять собой MJC.
  
  
  
  Формальное определение авторами статьи:
  

  $$

  $$

  $$

  $$

  Где $$ — стоимость продвижения во времени, желательно сделать его пропорциональным $$, стандартному отклонению распределения уровней в последовательностях, и обратно пропорциональным размеру сравниваемых рядов. $$ — управляющий параметр, чем меньше $$, тем эластичнее получается мера. При $$ прыжок будет совершён на самый близкий по значению уровень вне зависимости, где он находится; при $$ прыжок по сути всегда будет совершаться на точку с $$.
  
  Несложно заметить, что функция получилась асимметричной, но это можно исправить, если положить $$ = $$ $$ или $$ = $$
  
  $$ имеет смысл подбирать таким образом, чтобы избежать ситуации, когда ближайшей по $$ оказывается точка где-нибудь в конце ряда, и алгоритм «проскакивает» весь ряд (см. рисунок). Конкретные значения зависят от амплитуды значений $$ и $$.
  
  
  
  Собственно, коварное «в некотором смысле» парой абзацев выше относится именно к $$: $$ получилась перекошенной. На самом деле, не обязательно останавливаться на простом перевзвешивании евклидовой метрики. Почему бы не заменить $$ на $$ с корректированием $$? (Подумать, как это скажется на поведении $$ — задача для любопытного читателя ;))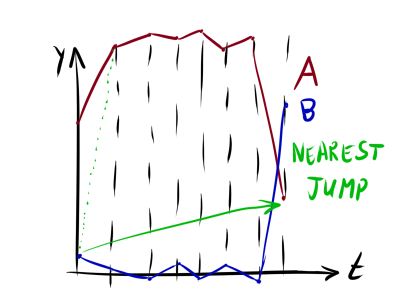
  
  MJC — развитие идеи евклидовой метрики с верхней границей на вклад отсчётов. Если в $$ выбросы вносят фикисрованный вклад, то в MJC играет роль предыстория ряда. В самом простом случае штраф возрастает квадратично. Более того, какой уровень считается выбросом для данной пары рядов, определяется автоматически. Полная история чуть сложнее, но будет не слишком большим искажением резюмировать, что MJC «прощает» единичные выбросы, но выдаёт большое значение чем $$, если в рядах есть длинные сильно различающиеся участки.
  
  
  
  Используйте MJC по умолчанию, когда известно, что ряды не «разьезжаются» во времени, так как чаще всего данные поражены именно белым шумом, а не группированными выбросами.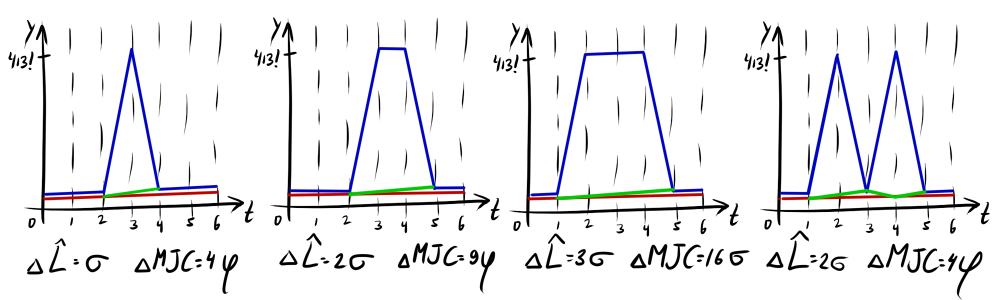
• Кросс-корреляция. Эту меру близости следует использовать когда особые точки и интервалы в рядах могут быть сдвинуты во времени друг от друга, но сдвиг фиксированный — внутреннее расстояние между важными элементами сохраняется. Характерные точки могут появляться и исчезать, плюс, сравниваемые временные ряды могут быть разной длительности. Отличный выбор, если известно, что структура последовательностей не искажена во времени («жёсткое» подобие по форме). Также в этом случае можно просто-напросто посчитать $$ для каждого возможного смещения одного ряда относительно другого.
  
  Изредка кросс-корреляция очень выручает, но, как правило, где смещение, там и искажения. Так что гораздо чаще используется…
• Динамическая трансформация временной шкалы (Dynamic Time Warping, DTW).
  
  Часто бывает так, что характерные части временных рядов не только отстоят друг от друга по оси времени, но ещё и растянуты или сжаты. Тогда ни евклидова метрика ни кросс-корреляция не дают показательных результатов.
  
  DTW-алгоритм строит матрицу возможных отображений одного ряда на другой, с учётом того, что отсчёты рядов могут как сдвигаться, так и изменять уровень. Путь в этой матрице с минимальным значением стоимости — и есть DTW-расстояние. Похожий принцип используется в алгоритме Вагнера-Фишера нахождения минимального редакционного расстояния между строками.
  
  Формальное описание алгоритма можно прочитать на Википедии, я же попробую полуформально пройти по основным пунктам. Возьмём две последовательности $$; $$. Они имеют похожую форму, но их пики смещены друг относительно друга. Посчитаем матрицу расстояний $$ между каждой парой уровней. На этом шаге обычно используется обычный $$ или $$. После чего построим матрицу трансформаций $$. Будем заполнять её слева-направо, сверху-вниз, по правилу $$. $$, для верхнего столбца и левого ряда части членов в $$ нет.
  
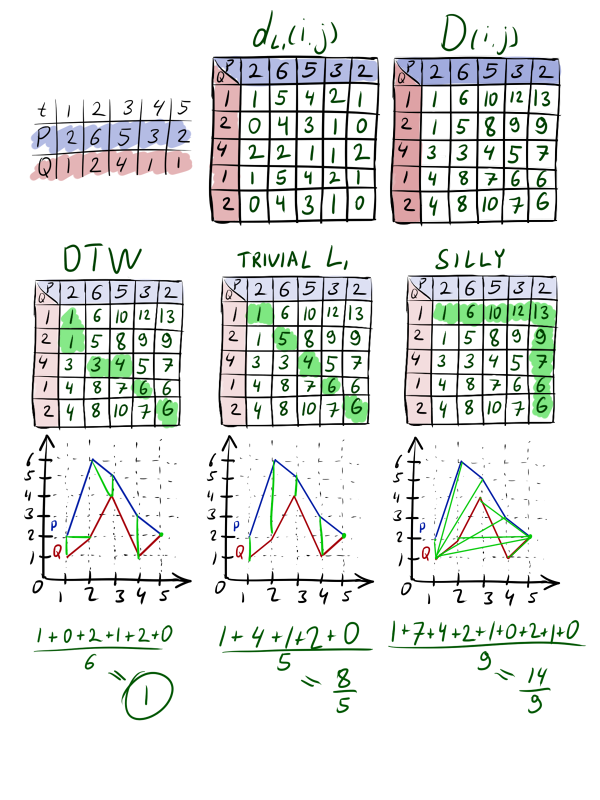
  Построим путь из $$ в $$, каждый раз переходя в клетку с как можно меньшим числом. Каждая посещённая клетка $$ будет означать, что при оптимальной трансформации точка $$ первого ряда отображается на $$-тую точку второго. Стоимость такой трансформации складывается из разницы между уровнями этих точек и стоимости оптимальной трансформации всех точек до этой пары. Можно сопоставлять одной точке несколько других, но двигаться будем только влево, вверх либо (желательно) влево-вверх, чтобы был прогресс.
  
  Таких путей можно построить много, но оптимальным из них будет тот, который минимизирует $$, где K — длина пути, а $$ — значение в матрице расстояний.
  
  DTW — замечательная функция для вычисления различия временных рядов, фактически baseline для сравнения c другими метриками. Она широко используется как в задачах сопоставления отрезков звука таки и при сопоставлении участков генома. Смело применяйте её, когда ряды должны быть похожи по форме, но ничего неизвестно про максимальную величину сдвига или искажения. Тем не менее, и у неё есть недостатки. Во-первых, она долго считается и/или требует дополнительной памяти, во-вторых DTW не всегда показывает адекватное расстояние, при добавлении в последовательность новых характерных точек. Что ещё хуже, не так просто прикинуть на глазок, как изменение одного из рядов скажется на пути по $$.
  
  Стоит упомянуть про функцию близости Edit Distance with Real Penalty (ERP) с похожим поведением, но более снисходительно относящуюся к отсчётам-выбросам, которые не удаётся сопоставить. Кроме того, нельзя обойти стороной Time Warp Edit Distance with Stiffness (TWED)[6]. Авторы этой метрики разработали более общий подход к описанию функций близости, основанных на операциях delete-match-insert (алгоритм Вагнера-Фишера снова передаёт привет), так что DTW и ERP — частные случаи TWED.
  
  ERP и TWED — параметрические; DTW — нет. С одной стороны, это удобно, с другой стороны иногда такая бесконечная эластичность вредит. Существует быстрая версия DTW, версия для разреженных данных, и огромное количество реализаций этого алгоритма.
• Длиннейший общий отрезок/длиннейшая общая подстрока (Longest Common Distance, LCD / Longest Common Subsequence, LCSS). LCSS находит применение в последовательностях, где значения отсчётов — метки классов, или где просто малое количество уровней. В последнем случае, LCSS можно модифицировать, чтобы находить длиннейший отрезок, на котором разность значений рядов меньше некоторого порога.
• Дискретное расстояние Фреше, оно же сцепленное расстояние. Полуформально объяснение звучит так: будем двигать точку A по последовательности P, а точку B — по Q, возможно неравномерно. В таком случае, расстоянием Фреше между P и Q будет минимально возможное расстояние между A и B, с которым можно провести обе точки через кривые. Бррр… лучше посмотрите пример с собакой на поводке в Википедии. В нашем случае $$, но возможны модификации. Подходит для редких случаев, когда известно, что в датасете нет отсчётов-выбросов, но есть вертикально смещённые друг относительно друга ряды одинаковой формы.
  
  Полезно сравнить между собой LCD и расстояние Фреше. Если в первом случае мы берём некоторый максимальный порог и смотрим, какой максимальный подотрезок можно пройти, не превышая его, то во втором мы проходим обе последовательности, и смотрим, какой минимальный порог нам для этого понадобился. Обе эти меры используются в задачах с подобием во времени, когда известна некоторая дополнительная информация.
• Расстояние с поправкой на сложность (Complexity Invariant Distance, CID)[7]
  
  Иногда бывает полезно вводить в метрику дополнительные факторы, помогающие разрешать спорные случаи. Например, бывает так, что ряды P и Q совпадают друг с другом на протяжении почти всего отрезка времени, но сильно отличаются в нескольких точках, а ряд R совсем не похож на ряд P по форме, но, тем не менее, близок к нему в среднем. Как правило, мы бы хотели считать P и Q как более похожие друг на друга.
  
  
  
  В качестве дополнительного фактора можно взять «сложность» последовательности. Если кривые P, Q и R имеют одинкавое попарное расстояние, но кривые P и Q вдобавок одинаковую «сложность», то будем счиать P и Q более похожими.
  
  «Сложность» можно измерять по-разному, но не забывайте, что этот параметр должен легко считаться, и иметь хорошую интерпретируемость. Авторы CID утверждают, что в среднем лучшие результаты выдаёт мера сложности, основанная на длине ломаной графика временного ряда:
  

  $$

  $$

  $$

  Где $$ — основная метрика (в статье использовалась евклидово расстояние). Для рядов с одинаковым расстоянием между отсчётами возможно упрощение — сумма квадратов производной:
  

  $$

  
  Авторы приводят в статье довольно странные примеры с серией чисел, образованной «обкаткой» плоской фигуры вокруг — не совсем конвенциональное использование рядов — но утверждают, что CID стабильно немного ($$) лучшает результаты и на других задачах.
• Расстояние с поправкой на взаимную компрессию (Compression Rate Distance, CRD)[8]
  
  Создатели CRD, применяют теоретико-информационный подход для модификации $$. Уровни последовательностей дискретизуются, затем используется функция информационной энтропии, чтобы посчитать насколько сложно восстановить $$, имея $$. Если нужно мало дополнительной информации, чтобы это сделать, то будем считать $$ и $$ более похожими друг на друга в контексте кластеризации. Вообще говоря, посчитать такую «взаимную архивируемость» можно разными способами, но самый простой — вычислить энтропию от их дискретизированной разности.
  

  $$

  $$

  $$

  $$

  И, наконец:

  $$

  или:

  $$

  Где $$ — степень влияния CRD, а $$ позволяет избежать деления на ноль. В качестве $$ в статье использовалась евклидова метрика. Авторы провели эксперименты с $$ и $$ на наборах данных с UCR Time Series Data Mining Site. Утверждается, что CRD в среднем рабоает немного лучше, чем просто евклидово расстояние ($$) и евклид с CID ($$). Также говорится, что евклидова метрика + CRD работает на тестовых датасетах чуть-чуть лучше, чем DTW, но представленные графики, на мой взгляд, не очень убедительны. Кроме того, авторы рассмотрели несколько дополнительных возможностей и свойств CID: ранний останов в вычислении расстояния, неравенство треугольника и нижнее ограничение на CID для децимированной последовательности.
  
  CRD-поправку можно использовать и как самостоятельную метрику в задаче кластеризации последовательностей символов, но вряд ли такое выйдет, когда $$ — действительная переменная. Дело в том, что CRD выдаёт малые значения, когда $$ и $$ имеют мало возможных уровней вертикального смещения друг относительно друга. При этом неважно, как именно расположены отсчёты этих рядов, для которых выполняется каждое отдельное отличие. Ряды на рисунках 1 и 2 имеют одинаковое значение CRD, так как и в том, и в другом случае их разность имеет ровно один уровень. Ряды на рисунках 3 и 4 тоже имеют одинаковый CRD, хоть и больший, чем в 1 и 2 случаях. Здесь есть два уровня возможной разницы. Неважно, как они расположены — последовательно или вразнобой. Заметьте, что CID бы показал, что в четвёртом случае красный график заметно сложнее синего.
  
  
  
  При использовании CRD играют важную роль выделение тренда и использование дополнительных предположений, за счёт которых можно «взаимно архивировать» ряды. Так, ряды на графиках 5 и 6 по умолчанию имеют одинаковое компрессионное расстояние, но если в шестом случае выделить тренд, картина изменится.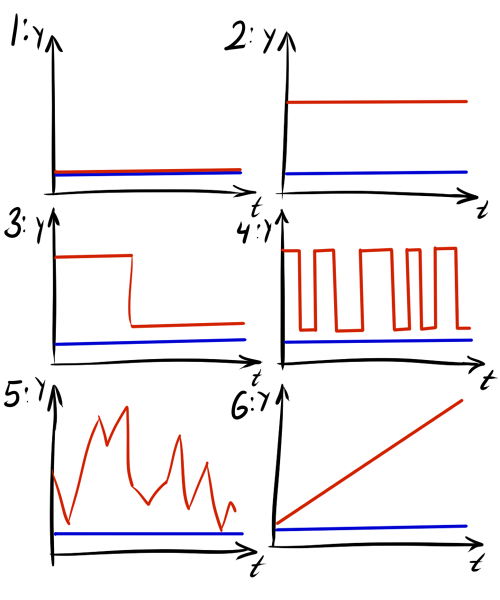
• Расстояние Махаланобиса[9]
  
  Не стоит забывать и про эту модификацию метрики, предложенной ещё в 1936 году. Индийский статистик Махаланобис использовал её совместно с евклидовой метрикой, чтобы вычислять рассояние между элементами выборки с поправкой на ковариацию элементов:
  

  $$

  Где S — матрица ковариаций. В случае диагональной матрицы ковариаций формула приобретает более простой вид:

  $$

  Отсюда легко видно, что переменные, дисперсия которых больше, вносят меньший вклад в итоговый показатель расстояния. На первый взгляд, не совсем понятно, причём здесь временный ряды. Однако поправка Махаланобиса позволяет разрешать ситуации, когда ряды состоят из интервалов двух типов: первый тип — значения последовательностей имеют малую дисперсию и хорошо структурированы, второй тип — значения имеют большой разброс и не несут смысловой нагрузки. Поправка Махаланобиса увеличивает вклад структурированных интервалов в расстояние между временными рядами.
  
  
  Как по мне, так всё равно странная идея, ведь Махаланобис предполагает, что все элементы происходят из одного распределения, но может пригодиться. Также нелишне будет упомянуть что существует аналогично модифицированная DTW-метрика.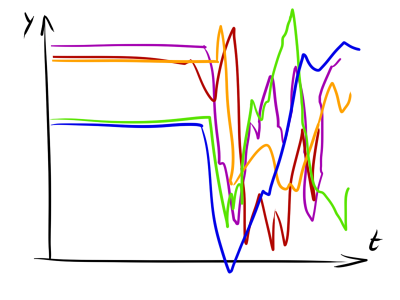

Заключение

Увы, я не нашёл адаптированных алгоритмов кластеризации последовательных данных, о которых бы было интересно поведать. Быть может, я чего-то не знаю, но несколько вечеров, проведённых в ArXiv и IEEE, не принесли мне прозрения. Складывается ощущение, что учёные ограничиваются лишь исследованием новых метрик для сравнения временных рядов, но не горят желанием изобретать специализированные алгоритмы. Вся хитрость происходит на этапе вычислении матрицы расстояний, а само разбиение на группы проводится старыми добрыми алгоритмами для статических данных: производные k-means, DBSCAN, Affinity propagation, тривиальная иерархическая кластеризация и прочими. Есть несколько, на которые можно взглянуть[10][11][12][13], но не то чтобы их результаты намного лучше старых методов.

K-means даёт приличные результаты реже, чем в случае статических данных. Некоторым исследователям удавалось успешно применять DBSCAN, но для него очень нетривиально подобрать хорошие параметры: основная область его применения — отнюдь не временные ряды. Гораздо интереснее выглядят два последних кандидата в списке, особенно часто применяется иерархическая кластеризация[14][15][16]. Также современные подходы предополагают вычисление и комбинирование нескольких матриц расстояния при помощи разных метрик.

Резюме. У вас в руках пачка временных рядов, и вы не знаете, что с ней делать?

Первым делом проверьте нет ли в данных пропущенных значений или явных отсчётов-выбросов. Затем попробуйте вывести часть датасета и посмотреть

• нет ли похожих, но сдвинутых во времени друг относительно друга графиков
• есть ли остчёты-выбросы, насколько систематически они встречаются
• есть ли графики с явно выраженной периодичностью
• есть ли типичные участки, когда дисперсия или скорость изменения рядов явно отличаются от других участков

Попробуйте собрать по рядам статистические данные и кластеризировать их; тут подойдут производные k-means. Если этого окажется недостаточно, посмотрите, имеют ли хоть какие то переменные явно бимодальное распределение (в частности, тренд) — это может помочь в понимании датасета.

Вычислите матрицу расстояний при помощи DTW или в несколько подходов TWED с разными параметрами. Выведите результат работы алгоритма иерархической кластеризации. Попытайтесь сформулировать гипотезу о форме датасета. Измените метрику по ситуации, или скомбинируйте несколько метрик. Повторите.

И самое главное: постарайтесь раздобыть знание о том, что, собственно, означают значения этих последовательностей. Это может коренным образом отразиться на выборе метрики.

Дааа… не то чтобы этот алгоритм сильно отличался от любой черновой обработки данных. Что поделать, кластеризация временных рядов — тяжкое занятие, и слишком многое зависит от конкретных данных. Надеюсь, моя статья хотя бы немного поможет, если вам придётся с ней столкнуться. В конце концов, даже небольшой прирост качества машинной обработки данных может означать для специалиста-человека разницу между «ничего не понятно» и «вроде можно нащупать закономерность».

Источники

[1] Saeed Aghabozorgi, Ali Seyed Shirkhorshidi, Teh Ying Wah — Time-series clustering – a Decade Review
[2] Konstantinos Kalpakis, Dhiral Gada, and Vasundhara Puttagunta — Distance Measures for Effective Clustering of ARIMA Time-Series.
[3] Subsequence Time Series (STS) Clustering Techniques for Meaningful Pattern Discovery
[4] Li Junkui, Wang Yuanzhen, Li Xinping — LB HUST: A Symmetrical Boundary Distance for Clustering Time Series
[5] Joan Serria, Josep Lluis Arcos — A Competitive Measure to Assess the Similarity Between Two Time Series
[6] P.F. Marteau — Time Warp Edit Distance with Stiffness Adjustment for Time Series Matching
[7] Gustavo E.A.P.A. Batista, Xiaoyue Wang, Eamonn J. Keogh — A Complexity-Invariant Distance Measure for Time Series
[8] Vo Thanh Vinh, Duong Tuan Anh — Compression Rate Distance Measure for Time Series
[9] Dinkar Sitaram, Aditya Dalwani, Anish Narang, Madhura Das, Prafullata Auradkar — A Measure Of Similarity Of Time Series Containing Missing Data Using the Mahalanobis Distance
[10] John Paparrizos, Luis Gravano — K-Shape: Efficient and Accurate Clustering of Time Series // Fast and Accurate Time-Series Clustering
[11] Leonardo N. Ferreiraa, Liang Zhaob — Time Series Clustering via Community Detection in Networks
[12] Zhibo Zhu, Qinke Peng, Xinyu Guan — A Time Series Clustering Method Based on Hypergraph Partitioning
[13] Shan Jicheng, Liu Weike — Clustering Algorithm for Time Series Based on Peak Interval
[14] Sangeeta Rani — Modified Clustering Algorithm for Time Series Data
[15] Pedro Pereira Rodrigues, Joao Gama, Joao Pedro Pedroso — Hierarchical Clustering of Time Series Data Streams
[16] Finding the Clusters with Potential Value in Financial Time Series based on Agglomerative Hierarchical Clustering
[17] Goktug T. Cinar and Jose C. Principe — Clustering of Time Seriess Using a Hierarchical Linear Dynamical System

Источник: habrahabr.ru

Комментарии: