Безытеративное обучение однослойного персептрона. Задача классификации
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2017-07-16 00:51
Я продолжаю цикл статей по разработке метода безытеративного обучения нейронных сетей. В этой статье будем обучать однослойный персептрон с сигмоидальной активационной ф-ей. Но этот метод можно применить для любых нелинейных биективных активационных ф-й с насыщением и первые производные которых симметричны относительно оси OY.
В прошлой статье мы рассмотрели метод обучения основанный на решении СЛАУ, решать ее мы не будем т.к. это слишком трудоемкий процесс. Сейчас нас интересует из этого метода только вектор «B», в этом векторе отражено насколько важен тот или иной признак для классификации.
И тут из-за того, что имеется активационная ф-я с насыщением можно выразить веса как: Первое, что необходимо сделать — это заменить на . Т.к. в задачи классификации «y» может быть либо 1(принадлежит), либо 0(не принадлежит). То t должно быть либо 1, либо -1. Отсюда . Теперь
Теперь выразим коэффициент «K» как дробь, где в числителе функция, обратная ф-и активации от 0.99(от единицы взять нельзя т.к. будет +бесконечность), а в знаменателе усредненное значение модулей всех элементов входящих в выборку(вероятно, можно использовать квадратный корень из усредненной энергии). И умножается все это на -1.
Итоговая формула получается:
Для сигмоиды, которая имеет вид , обратная ф-я — , при
*Небольшая проверка
Пусть есть две пары . Рассчитаем веса по формуле приведенной выше:
Теперь «прогоним» наши вектора через получившийся нейрон, напомню формулу отклика нейрона: Первый вектор дал результат 0.997, второй — , что очень похоже на правду.
*Тестирование
Для тестирования была взята обучающая выборка 2 сигнала без шума, 1 и 2 Гц, 200 отсчетов. Одному герцу соответствует отклик НС {0,1}, двум {1,0}.
Во время тестирования распознавался сигнал + гауссов шум. ОСШ = 0.33
Ниже представлено распознавание:
1Гц, самый хороший результат

2 Гц, самый хороший результат
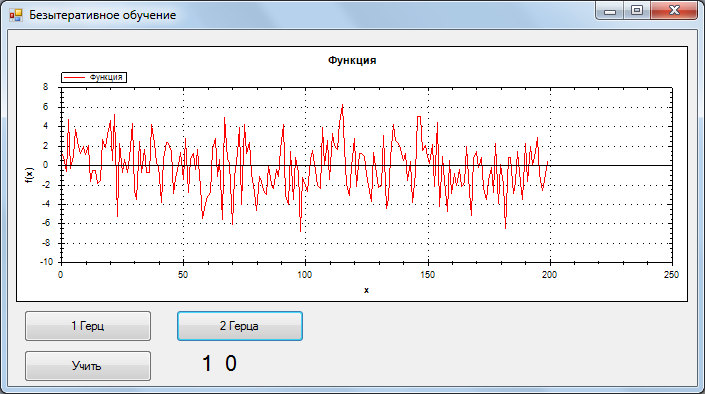
1 Гц, самый плохой результат
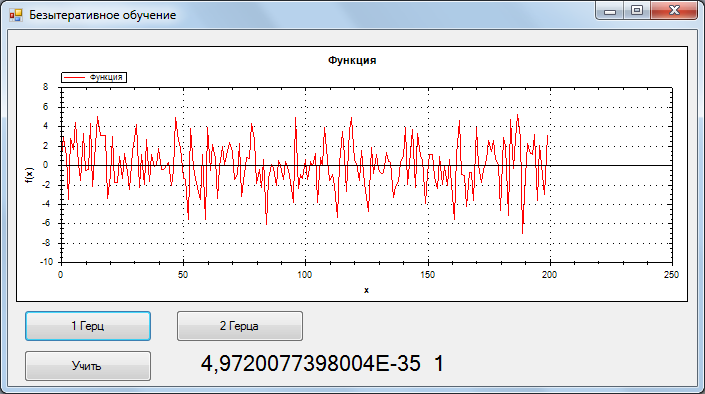
Учитывая, то что точность очень высокая(тестировал и на других сигналах). Я предполагаю, что данный метод сводит функцию ошибки в глобальный минимум.
Код обучения:
В дальнейших статьях планирую рассмотреть, обучение многослойных сетей, генерацию сетей с оптимальной архитектурой и обучение сверточных сетей.
В прошлой статье мы рассмотрели метод обучения основанный на решении СЛАУ, решать ее мы не будем т.к. это слишком трудоемкий процесс. Сейчас нас интересует из этого метода только вектор «B», в этом векторе отражено насколько важен тот или иной признак для классификации.
И тут из-за того, что имеется активационная ф-я с насыщением можно выразить веса как: Первое, что необходимо сделать — это заменить на . Т.к. в задачи классификации «y» может быть либо 1(принадлежит), либо 0(не принадлежит). То t должно быть либо 1, либо -1. Отсюда . Теперь
Теперь выразим коэффициент «K» как дробь, где в числителе функция, обратная ф-и активации от 0.99(от единицы взять нельзя т.к. будет +бесконечность), а в знаменателе усредненное значение модулей всех элементов входящих в выборку(вероятно, можно использовать квадратный корень из усредненной энергии). И умножается все это на -1.
Итоговая формула получается:
Для сигмоиды, которая имеет вид , обратная ф-я — , при
*Небольшая проверка
Пусть есть две пары . Рассчитаем веса по формуле приведенной выше:
Теперь «прогоним» наши вектора через получившийся нейрон, напомню формулу отклика нейрона: Первый вектор дал результат 0.997, второй — , что очень похоже на правду.
*Тестирование
Для тестирования была взята обучающая выборка 2 сигнала без шума, 1 и 2 Гц, 200 отсчетов. Одному герцу соответствует отклик НС {0,1}, двум {1,0}.
Во время тестирования распознавался сигнал + гауссов шум. ОСШ = 0.33
Ниже представлено распознавание:
1Гц, самый хороший результат

2 Гц, самый хороший результат

1 Гц, самый плохой результат

Учитывая, то что точность очень высокая(тестировал и на других сигналах). Я предполагаю, что данный метод сводит функцию ошибки в глобальный минимум.
Код обучения:
public void Train(Vector[] inp, Vector[] outp) { OutNew = new Vector[outp.Length]; In = new Vector[outp.Length]; Array.Copy(outp, OutNew, outp.Length); Array.Copy(inp, In, inp.Length); for (int i = 0; i < OutNew.Length; i++) { OutNew[i] = 2*OutNew[i]-1; } K = 4.6*inp[0].N*inp.Length; double summ = 0; for (int i = 0; i < inp.Length; i++) { summ += Functions.Summ(MathFunc.abs(In[i])); } K /= summ; Parallel.For(0, _neurons.Length, LoopTrain); } void LoopTrain(int i) { for (int k = 0; k < In[0].N; k++) { for (int j = 0; j < OutNew.Length; j++) { _neurons[i].B.Vecktor[k] += OutNew[j].Vecktor[i]*In[j].Vecktor[k]; } } _neurons[i].W = K*_neurons[i].B; }В дальнейших статьях планирую рассмотреть, обучение многослойных сетей, генерацию сетей с оптимальной архитектурой и обучение сверточных сетей.
Источник: habrahabr.ru