Автоэнкодеры в Keras, Часть 1: Введение

Во время погружения в Deep Learning зацепила меня тема автоэнкодеров, особенно с точки зрения генерации новых объектов. Стремясь улучшить качество генерации, читал различные блоги и литературу на тему генеративных подходов. В результате набравшийся опыт решил облечь в небольшую серию статей, в которой постарался кратко и с примерами описать все те проблемные места с которыми сталкивался сам, заодно вводя в синтаксис Keras.

Автоэнкодеры

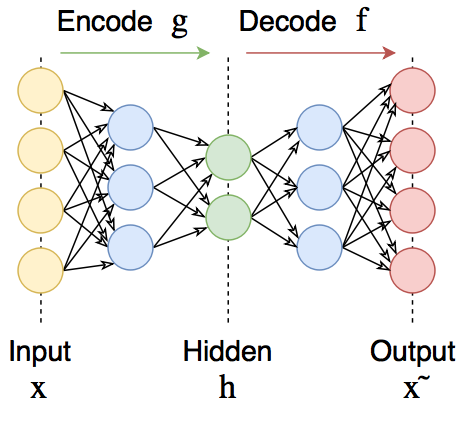
Автоэнкодеры — это нейронные сети прямого распространения, которые восстанавливают входной сигнал на выходе. Внутри у них имеется скрытый слой, который представляет собой код, описывающий модель. Автоэнкодеры конструируются таким образом, чтобы не иметь возможность точно скопировать вход на выходе. Обычно их ограничивают в размерности кода (он меньше, чем размерность сигнала) или штрафуют за активации в коде. Входной сигнал восстанавливается с ошибками из-за потерь при кодировании, но, чтобы их минимизировать, сеть вынуждена учиться отбирать наиболее важные признаки.



Кому интересно, добро пожаловать под кат


Автоэнкодеры состоят из двух частей: энкодера и декодера . Энкодер переводит входной сигнал в его представление (код): , а декодер восстанавливает сигнал по его коду: .

Автоэнкодер, изменяя и , стремится выучить тождественную функцию , минимизируя какой-то функционал ошибки.
 

При этом семейства функций энкодера и декодера как-то ограничены, чтобы автоэнкодер был вынужден отбирать наиболее важные свойства сигнала.

Сама по себе способность автоэнкодеров сжимать данные используется редко, так как обычно они работают хуже, чем вручную написанные алгоритмы для конкретных типов данных вроде звуков или изображений. А также для них критически важно, чтобы данные принадлежали той генеральной совокупности, на которой сеть обучалась. Обучив автоэнкодер на цифрах, его нельзя применять для кодирования чего-то другого (например, человеческих лиц).

Однако автоэнкодеры можно использовать для предобучения, например, когда стоит задача классификации, а размеченных пар слишком мало. Или для понижения размерности в данных для последующей визуализации. Либо когда просто надо научиться различать полезные свойства входного сигнала.

Более того, некоторые их развития (о которых тоже будет написано далее), такие как вариационный автоэнкодер (VAE), а также его сочетание с состязающимися генеративным сетями (GAN), дают очень интересные результаты и находятся сейчас на переднем крае науки о генеративных моделях.
 

Keras

Keras — это очень удобная высокоуровневая библиотека для глубокого обучения, работающая поверх theano или tensorflow. В ее основе лежат слои, соединяя которые между собой, получаем модели. Созданные однажды модели и слои сохраняют в себе свои внутренние параметры, и потому, например, можно обучить слой в одной модели, а использовать его уже в другой, что очень удобно.

Модели keras легко сохранять/загружать, у них простой, но в тоже время глубоко настраиваемый процесс обучения; модели свободно встраиваются в tensorflow/theano код (как операции над тензорами).

В качестве данных будем использовать датасет рукописных цифр MNIST

Загрузим его:
 

from keras.datasets import mnist
import numpy as np

(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.astype('float32') / 255.
x_test  = x_test .astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test  = np.reshape(x_test,  (len(x_test),  28, 28, 1))

Сжимающий автоэнкодер

Для начала создадим наиболее простой (сжимающий, undercomplete) автоэнкодер с кодом малой размерности из двух полносвязных слоев: енкодера и декодера.

Так как интенсивность цвета нормирована на единицу, то активацию выходного слоя возьмем сигмоидой.

Напишем отдельные модели для энкодера, декодера и целого автоэнкодера. Для этого создадим экземпляры слоев и применим их один за другим, в конце все объединив в модели.
 

from keras.layers import Input, Dense, Flatten, Reshape
from keras.models import Model

def create_dense_ae():
    # Размерность кодированного представления
    encoding_dim = 49

    # Энкодер
    # Входной плейсхолдер
    input_img = Input(shape=(28, 28, 1)) # 28, 28, 1 - размерности строк, столбцов, фильтров одной картинки, без батч-размерности
    # Вспомогательный слой решейпинга
    flat_img = Flatten()(input_img)
    # Кодированное полносвязным слоем представление
    encoded = Dense(encoding_dim, activation='relu')(flat_img)
    
    # Декодер
    # Раскодированное другим полносвязным слоем изображение
    input_encoded = Input(shape=(encoding_dim,))
    flat_decoded = Dense(28*28, activation='sigmoid')(input_encoded)
    decoded = Reshape((28, 28, 1))(flat_decoded)

    # Модели, в конструктор первым аргументом передаются входные слои, а вторым выходные слои
    # Другие модели можно так же использовать как и слои
    encoder = Model(input_img, encoded, name="encoder")
    decoder = Model(input_encoded, decoded, name="decoder")
    autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
    return encoder, decoder, autoencoder

Создадим и скомпилируем модель (под компиляцией в данном случае понимается построение графа вычислений обратного распространения ошибки)
 

encoder, decoder, autoencoder = create_dense_ae()
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

Посмотрим на число параметров
 

autoencoder.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
encoder (Model)              (None, 49)                38465     
_________________________________________________________________
decoder (Model)              (None, 28, 28, 1)         39200     
=================================================================
Total params: 77,665.0
Trainable params: 77,665.0
Non-trainable params: 0.0
_________________________________________________________________

Обучим теперь наш автоэнкодер
 

autoencoder.fit(x_train, x_train,
                epochs=50,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

Epoch 46/50
60000/60000 [==============================] - 3s - loss: 0.0785 - val_loss: 0.0777
Epoch 47/50
60000/60000 [==============================] - 2s - loss: 0.0784 - val_loss: 0.0777
Epoch 48/50
60000/60000 [==============================] - 3s - loss: 0.0784 - val_loss: 0.0777
Epoch 49/50
60000/60000 [==============================] - 2s - loss: 0.0784 - val_loss: 0.0777
Epoch 50/50
60000/60000 [==============================] - 3s - loss: 0.0784 - val_loss: 0.0777

Функция отрисовки цифр
 

%matplotlib inline
import seaborn as sns
import matplotlib.pyplot as plt

def plot_digits(*args):
    args = [x.squeeze() for x in args]
    n = min([x.shape[0] for x in args])
    
    plt.figure(figsize=(2*n, 2*len(args)))
    for j in range(n):
        for i in range(len(args)):
            ax = plt.subplot(len(args), n, i*n + j + 1)
            plt.imshow(args[i][j])
            plt.gray()
            ax.get_xaxis().set_visible(False)
            ax.get_yaxis().set_visible(False)

    plt.show()

Закодируем несколько изображений и, ради интереса, взглянем на пример кода
 

n = 10

imgs = x_test[:n]
encoded_imgs = encoder.predict(imgs, batch_size=n)
encoded_imgs[0]

array([  6.64665604,   7.53528595,   3.81508064,   4.66803837,
         1.50886345,   5.41063929,   9.28293324,  10.79530716,
         0.39599913,   4.20529413,   6.53982353,   5.64758158,
         5.25313473,   1.37336707,   9.37590599,   6.00672245,
         4.39552879,   5.39900637,   4.11449528,   7.490417  ,
        10.89267063,   7.74325705,  13.35806847,   3.59005809,
         9.75185394,   2.87570286,   3.64097357,   7.86691713,
         5.93383646,   5.52847338,   3.45317888,   1.88125253,
         7.471385  ,   7.29820824,  10.02830505,  10.5430584 ,
         3.2561543 ,   8.24713707,   2.2687614 ,   6.60069561,
         7.58116722,   4.48140812,   6.13670635,   2.9162209 ,
         8.05503941,  10.78182602,   4.26916027,   5.17175484,   6.18108797], dtype=float32)

Декодируем эти коды и сравним с оригиналами
 

decoded_imgs = decoder.predict(encoded_imgs, batch_size=n)

plot_digits(imgs, decoded_imgs)

Глубокий автоэнкодер

Никто не мешает нам сделать такой же автоэнкодер, но с большим числом слоев. В таком случае он сможет вычленять более сложные нелинейные закономерности
 

def create_deep_dense_ae():
    # Размерность кодированного представления
    encoding_dim = 49

    # Энкодер
    input_img = Input(shape=(28, 28, 1))
    flat_img = Flatten()(input_img)
    x = Dense(encoding_dim*3, activation='relu')(flat_img)
    x = Dense(encoding_dim*2, activation='relu')(x)
    encoded = Dense(encoding_dim, activation='linear')(x)
    
    # Декодер
    input_encoded = Input(shape=(encoding_dim,))
    x = Dense(encoding_dim*2, activation='relu')(input_encoded)
    x = Dense(encoding_dim*3, activation='relu')(x)
    flat_decoded = Dense(28*28, activation='sigmoid')(x)
    decoded = Reshape((28, 28, 1))(flat_decoded)
    
    # Модели
    encoder = Model(input_img, encoded, name="encoder")
    decoder = Model(input_encoded, decoded, name="decoder")
    autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
    return encoder, decoder, autoencoder

d_encoder, d_decoder, d_autoencoder = create_deep_dense_ae()
d_autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

Посмотрим на summary нашей модели
 

d_autoencoder.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_3 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
encoder (Model)              (None, 49)                134750    
_________________________________________________________________
decoder (Model)              (None, 28, 28, 1)         135485    
=================================================================
Total params: 270,235.0
Trainable params: 270,235.0
Non-trainable params: 0.0

Число параметров выросло более чем в 3 раза, посмотрим, справится ли новая модель лучше:
 

d_autoencoder.fit(x_train, x_train,
                  epochs=100,
                  batch_size=256,
                  shuffle=True,
                  validation_data=(x_test, x_test))

Epoch 96/100
60000/60000 [==============================] - 3s - loss: 0.0722 - val_loss: 0.0724
Epoch 97/100
60000/60000 [==============================] - 3s - loss: 0.0722 - val_loss: 0.0719
Epoch 98/100
60000/60000 [==============================] - 3s - loss: 0.0721 - val_loss: 0.0722
Epoch 99/100
60000/60000 [==============================] - 3s - loss: 0.0721 - val_loss: 0.0720
Epoch 100/100
60000/60000 [==============================] - 3s - loss: 0.0721 - val_loss: 0.0720

n = 10

imgs = x_test[:n]
encoded_imgs = d_encoder.predict(imgs, batch_size=n)
encoded_imgs[0]

decoded_imgs = d_decoder.predict(encoded_imgs, batch_size=n)

plot_digits(imgs, decoded_imgs)

Видим, что лосс насыщается на значительно меньшей величине, да и циферки немного более приятные
 

Сверточный автоэнкодер

Так как мы работаем с картинками, в данных должна присутствовать некоторая пространственная инвариантность. Попробуем этим воспользоваться: построим сверточный автоэнкодер
 

from keras.layers import Conv2D, MaxPooling2D, UpSampling2D

def create_deep_conv_ae():
    input_img = Input(shape=(28, 28, 1))

    x = Conv2D(128, (7, 7), activation='relu', padding='same')(input_img)
    x = MaxPooling2D((2, 2), padding='same')(x)
    x = Conv2D(32, (2, 2), activation='relu', padding='same')(x)
    x = MaxPooling2D((2, 2), padding='same')(x)
    encoded = Conv2D(1, (7, 7), activation='relu', padding='same')(x)

    # На этом моменте представление  (7, 7, 1) т.е. 49-размерное

    input_encoded = Input(shape=(7, 7, 1))
    x = Conv2D(32, (7, 7), activation='relu', padding='same')(input_encoded)
    x = UpSampling2D((2, 2))(x)
    x = Conv2D(128, (2, 2), activation='relu', padding='same')(x)
    x = UpSampling2D((2, 2))(x)
    decoded = Conv2D(1, (7, 7), activation='sigmoid', padding='same')(x)

    # Модели
    encoder = Model(input_img, encoded, name="encoder")
    decoder = Model(input_encoded, decoded, name="decoder")
    autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
    return encoder, decoder, autoencoder

c_encoder, c_decoder, c_autoencoder = create_deep_conv_ae()
c_autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

c_autoencoder.summary()

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_5 (InputLayer)         (None, 28, 28, 1)         0         
_________________________________________________________________
encoder (Model)              (None, 7, 7, 1)           24385     
_________________________________________________________________
decoder (Model)              (None, 28, 28, 1)         24385     
=================================================================
Total params: 48,770.0
Trainable params: 48,770.0
Non-trainable params: 0.0

c_autoencoder.fit(x_train, x_train,
                epochs=64,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

Epoch 60/64
60000/60000 [==============================] - 24s - loss: 0.0698 - val_loss: 0.0695
Epoch 61/64
60000/60000 [==============================] - 24s - loss: 0.0699 - val_loss: 0.0705
Epoch 62/64
60000/60000 [==============================] - 24s - loss: 0.0699 - val_loss: 0.0694
Epoch 63/64
60000/60000 [==============================] - 24s - loss: 0.0698 - val_loss: 0.0691
Epoch 64/64
60000/60000 [==============================] - 24s - loss: 0.0697 - val_loss: 0.0693

n = 10

imgs = x_test[:n]
encoded_imgs = c_encoder.predict(imgs, batch_size=n)
decoded_imgs = c_decoder.predict(encoded_imgs, batch_size=n)

plot_digits(imgs, decoded_imgs)

Несмотря на то, что количество параметров у этой сети намного меньше чем у полносвязных сетей, функция ошибки насыщается на значительно меньшей величине.
 

Denoising автоэнкодер

Автоэнкодеры можно обучить убирать шум из данных: для этого надо на вход подавать зашумленные данные и на выходе сравнивать с данными без шума:
 

где — зашумленные данные.

В Keras можно оборачивать произвольные операции из нижележащего фреймворка в Lambda слой. Обращаться к операциям из tensorflow или theano можно через модуль backend.

Создадим модель, которая будет зашумлять входное изображение, а избавлять от шума переобучим какой-либо из уже созданных автоэнкодеров.
 

import keras.backend as K
from keras.layers import Lambda

batch_size = 16

def create_denoising_model(autoencoder):
    def add_noise(x):
        noise_factor = 0.5
        x = x + K.random_normal(x.get_shape(), 0.5, noise_factor)
        x = K.clip(x, 0., 1.)
        return x

    input_img  = Input(batch_shape=(batch_size, 28, 28, 1))
    noised_img = Lambda(add_noise)(input_img)

    noiser = Model(input_img, noised_img, name="noiser")
    denoiser_model = Model(input_img, autoencoder(noiser(input_img)), name="denoiser")
    return noiser, denoiser_model


noiser, denoiser_model = create_denoising_model(autoencoder)
denoiser_model.compile(optimizer='adam', loss='binary_crossentropy')

denoiser_model.fit(x_train, x_train,
                   epochs=200,
                   batch_size=batch_size,
                   shuffle=True,
                   validation_data=(x_test, x_test))

n = 10

imgs = x_test[:batch_size]
noised_imgs = noiser.predict(imgs, batch_size=batch_size)
encoded_imgs = encoder.predict(noised_imgs[:n],  batch_size=n)
decoded_imgs = decoder.predict(encoded_imgs[:n], batch_size=n)

plot_digits(imgs[:n], noised_imgs, decoded_imgs)

Цифры на зашумленных изображениях с трудом проглядываются, однако denoising autoencoder неплохо убрал шум и цифры стали вполне читаемыми.
 

Разреженный (Sparse) автоэнкодер

Разреженный автоэнкодер — это просто автоэнкодер, у которого в функцию потерь добавлен штраф за величины значений в коде, то есть автоэнкодер стремится минимизировать такую функцию ошибки:
 

где — код,

— обычный регуляризатор (например L1):
 

Разреженный автоэнкодер не обязательно сужается к центру. Его код может иметь и большую размерность, чем входной сигнал. Обучаясь приближать тождественную функцию , он учится в коде выделять полезные свойства сигнала. Из-за регуляризатора даже расширяющийся к центру разреженный автоэнкодер не может выучить тождественную функцию напрямую.
 

from keras.regularizers import L1L2

def create_sparse_ae():
    encoding_dim = 16
    lambda_l1 = 0.00001
    
    # Энкодер
    input_img = Input(shape=(28, 28, 1))
    flat_img = Flatten()(input_img)
    x = Dense(encoding_dim*3, activation='relu')(flat_img)
    x = Dense(encoding_dim*2, activation='relu')(x)
    encoded = Dense(encoding_dim, activation='linear', activity_regularizer=L1L2(lambda_l1))(x)
    
    # Декодер
    input_encoded = Input(shape=(encoding_dim,))
    x = Dense(encoding_dim*2, activation='relu')(input_encoded)
    x = Dense(encoding_dim*3, activation='relu')(x)
    flat_decoded = Dense(28*28, activation='sigmoid')(x)
    decoded = Reshape((28, 28, 1))(flat_decoded)
    
    # Модели
    encoder = Model(input_img, encoded, name="encoder")
    decoder = Model(input_encoded, decoded, name="decoder")
    autoencoder = Model(input_img, decoder(encoder(input_img)), name="autoencoder")
    return encoder, decoder, autoencoder

s_encoder, s_decoder, s_autoencoder = create_sparse_ae()
s_autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

s_autoencoder.fit(x_train, x_train,
                epochs=400,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

Взглянем на коды
 

n = 10

imgs = x_test[:n]
encoded_imgs = s_encoder.predict(imgs, batch_size=n)
encoded_imgs[1]

array([  7.13531828,  -0.61532277,  -5.95510817,  12.0058918 ,
        -1.29253936,  -8.56000137,  -7.48944521,  -0.05415952,
        -2.81205249,  -8.4289856 ,  -0.67815018, -11.19531345,
        -3.4353714 ,   3.18580866,  -0.21041733,   4.13229799], dtype=float32)

decoded_imgs = s_decoder.predict(encoded_imgs, batch_size=n)

plot_digits(imgs, decoded_imgs)

Посмотрим, можно ли как-то интерпретировать размерности в кодах.
Возьмем среднее из всех кодов, а потом по очереди каждую размерность в усредненном коде заменим на максимальное ее значение.
 

imgs = x_test
encoded_imgs = s_encoder.predict(imgs, batch_size=16)
codes = np.vstack([encoded_imgs.mean(axis=0)]*10)
np.fill_diagonal(codes, encoded_imgs.max(axis=0))

decoded_features = s_decoder.predict(codes, batch_size=16)
plot_digits(decoded_features)

Какие-то черты проглядываются, но ничего толкового тут не видно.

Значения в кодах по одиночке никакого очевидного смысла не несут, лишь хитрое взаимодействие между значениями, происходящее в слоях декодера, позволяет ему по коду восстановить входной сигнал.

Можно ли из кодов генерировать объекты по собственному желанию?

Для того, чтобы ответить на этот вопрос, следует лучше изучить, что такое коды, и как их можно интепретировать. Про это в следующей части.
 

Полезные ссылки и литература

Этот пост основан на собственной интерпретации первой части поста создателя Keras Francois Chollet про автоэнкодеры в Keras.

А также главы про автоэнкодеры в Deep Learning Book.

Источник: habrahabr.ru

Комментарии: